Overview
We are studying the oscillation of atmospheric νμ into ντ. The disappearance of νμ has been observed already by several experiments, among them IceCube, and is a fairly well-measured phenomena (even though the neutrino mixing angle θ23 related to that measurement is the angle which we currently know with the least precision). However, the appearance of the ντ from a νμ source is much harder to measure.
The difficulty of measuring ντ appearance stems from the fact that in order for a ντ to undergo a charged current interaction, it needs to have enough energy to be able to produce a τ lepton (which requires roughly 1.8 GeV, about twice the proton mass!), and to have large enough interaction probability we would want even more energy than the bare minimum.

Oscillation probabilities for atmospheric νµ → νµ and νµ → ντ as a function of neutrino energy, for neutrinos crossing the full earth diameter and assuming sin2(2θ13) = 0.1. From Mena, et al. arXiv 0803.3044v2.
Due to the high energy required and because neutrino oscillations depend on L/E (L is the neutrino propagation distance and E is the neutrino energy), with the νμ disappearance first minimum being at L/E ~ 500 km/GeV it is clear that long or very-long oscillation baselines are required in addition to a high energy neutrino source. Neutrinos produced in the atmosphere fit the bill nicely. For instance, for neutrinos crossing the earth’s diameter the energy of the first maximum of ντ appearance is at 25 GeV (see figure). The use of atmospheric neutrinos to do this measurement therefore is quite natural given that a part of the νμ is produced at the correct energy range and the source is distant enough that we can measure the ντ appearance at its maximum.
In DeepCore we expect to be able to measure a few thousand ντ per year thanks to the large size of the detector, but unfortunately with a large νe and νμ background that hides the oscillation signal. In PINGU, while we do not expect to detect more neutrinos, we do expect to be able to reject a much larger fraction of the νμ background.
Unitarity of the neutrino mixing matrix and hints of new physics
In the Standard Model, there are 3 families of neutrinos (νe, νμ and ντ), each associated with charged leptons (e, μ and τ, respectively) through charged-current weak interaction. In order to have neutrino oscillation, it is required that the flavor eigenstates (νe, νμ and ντ) are not the same as the mass eigenstates (ν1, ν2 and ν3). Therefore, the neutrino interaction and propagation do not act in the same basis (see figure below), and there is a rotation matrix U to project the mass basis into the flavor basis.

Scheme of the νμ production at the atmosphere (via decay of charged π), its propagation (here shown as if in vacuum for simplification) and finally deep inelastic interaction at the detector through charged current (this is what will typically happen for the energy range considered here). The oscillation exists only thanks to the change on basis during the “propagation” stage. If instead of vacuum there was matter (which is the case for our measurement) the oscillation probabilities would change, and there would be some effect due to interaction with matter, but the overall figure would be the same.
In the 3-flavor neutrino oscillation, it is only possible to oscillate towards one of the 3 neutrino families mentioned previously, that is P(νμ → νe) + P(νμ → νμ) + P(νμ → ντ) = 1 at any given instant. If we measure each of these terms independently, we can then verify that their sum is 1 as expected.
If, when doing the experiment, we measure that these probabilities do not add up to 1, this would mean that there is at least one other neutrino flavor, let’s call it νs, that needs to exist with P(νμ → νe) + P(νμ → νμ) + P(νμ → ντ) + P(νμ → νs) = 1.
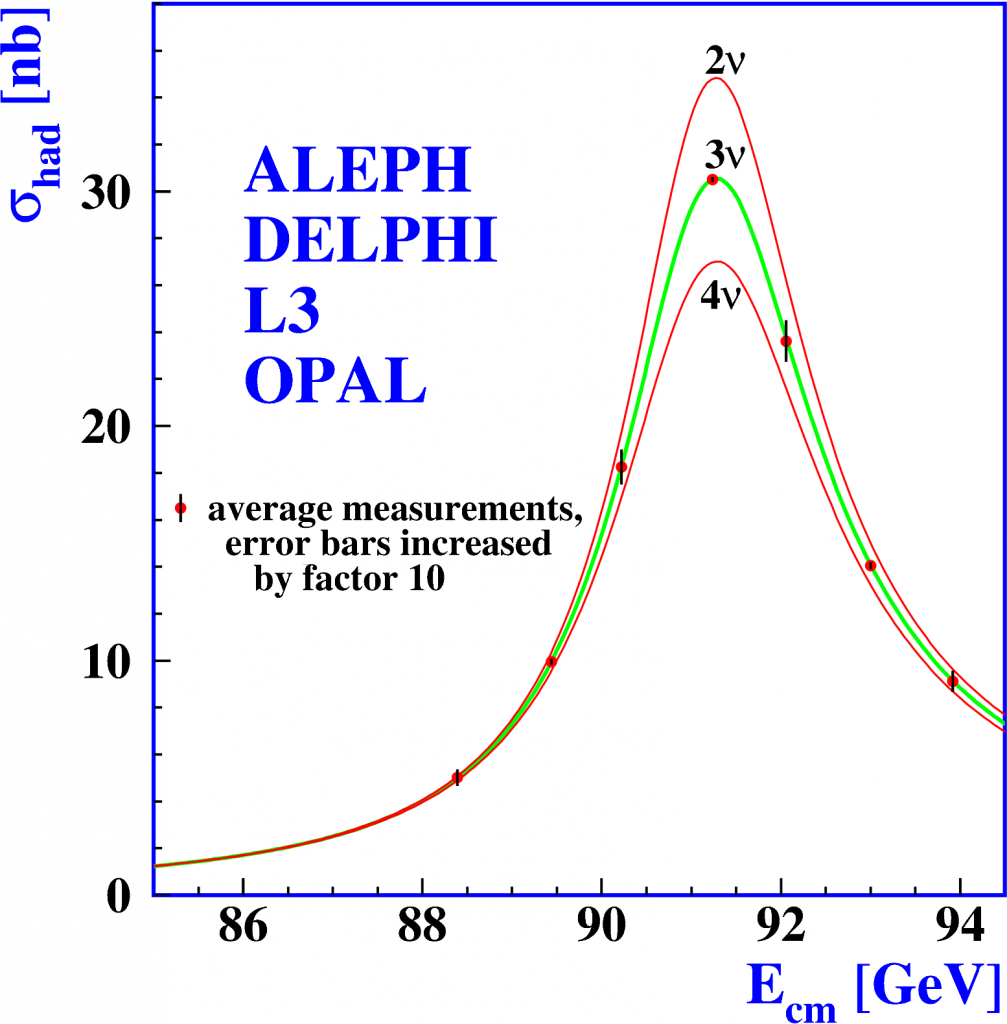
Measurement of the hadron production cross-section around Z resonance at the LEP. The curves show the predicted cross-section for 2, 3 and 4 ν species interacting with the Z boson. From Abdallah et al., Physics Reports 427, 257 (2006) [arXiv hep-ex/0509008].
This new neutrino flavor νs would be something completely new in the Standard Model because, through measures of the cross-section of the Z boson, we know it only couples to 3 families of light neutrino (see figure). Therefore the additional neutrino would not interact through the weak interaction, as the other neutrinos do. Since the Standard Model neutrinos interact only through weak interaction, these new neutrinos would not interact with matter (they would through gravitational interaction, but that is completely negligible) which is why these possible new neutrinos are commonly called “sterile neutrinos.”