Netflix is an American provider of on-demand Internet streaming media, its recommendation system conducts the task of making automatic predictions about the interests of a user by collecting taste information from many users.
Netflix Problem:
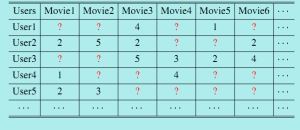
There is one training data set, 480,189 users and 17,770 movies are given, ratings Mij: user i rates movie j from 1 to 5, only 100,480,507 ratings is known. Average user rated over 200 movies and the average movie was rated by over 5000 users.
The data looks like this:
Matrix Factorization Method:
This method map both users and items to a joint latent factor space of dimensional f, such that user- item interactions are modeled as inner product in that space. Accordingly, each item i is associated with a vector qi , each user u is associated with a vector pu
For a given item i , the elements of qi measures the extent to which the item possesses those factors, positive or negative.
For a given user u, the elements of pu measure the extent of interest the user has in items that are high on the corresponding factors, again, positive or negative.
The resulting dot product qi*pu , captures the interaction between user u and item i– the user’s overall interest in the item’s characteristics. This is the approximation which we will use.
rui=qiTpu as the i,j th component of the audience-movie preference matrix.
Low rank structure
Because the preference of user will only depend on several factors, such as the theme of the movie, the actors, directors, etc…we believe the Matrix represent the flavor of audience is intrinsically low rank.
And the SVD(singular value decomposition)of our matrix may look like:
Models
So, our problem can be formulated in such mathematical way:
but, if we want to do the minimization on rank, it will be a NP problem, so instead, we do the minimization on another norm, so called Nuclear Norm, where the mathematical definition is the sum of all singular values:
http://mahout.apache.org/users/recommender/matrix-factorization.html