The specific tenets of quantum mechanics are undoubtedly mind-boggling. Its transgressions on Einstein’s Theory of Special Relativity combined with its probabilistic nature render it almost inconceivable. Perhaps more inconceivable, however, is the idea that quantum mechanics dictates a uniquely human relationship with nature, one that places the long-avoided, subjective notion of consciousness in the objective scientific domain.

Humans as Observers

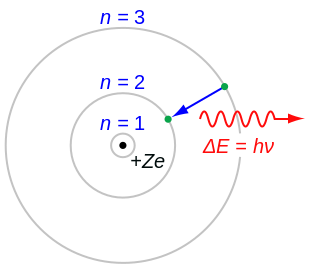
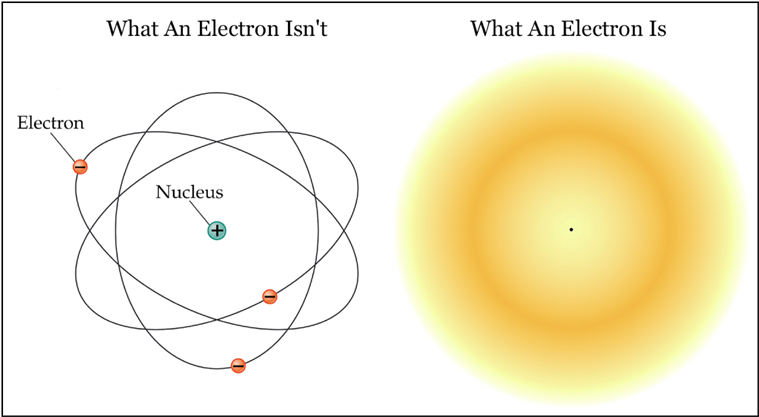
Recall that any unobserved object exhibits a superposition, having a distinct probability of existing in every temporal and spatial point until an observation of the object results in a superposition collapse (or decoherence), with larger objects simply being more unlikely—not impossible—to spontaneously tunnel through space and time. Observations typically take the form of pieces of equipment or measuring devices capturing the state of an atom or the location of the electron, but such tools are the product of human ingenuity and have their “findings” confirmed only upon human intervention.

Why does nature “choose” to revert to a distinct position or configuration exclusively when humans perform observations or measurements? Why does it not do so in the ubiquitous presence of inanimate atoms and subatomic particles? Such a phenomenon may not be a “choice” of nature but rather the result of a unique relationship between the laws of physics and human consciousness. After all, how can we definitively draw conclusions regarding the laws of nature if we are unaware of them? They may in fact exist, but to each individual oblivious of them, the lack of their projection into one’s mind warrants their nonexistence.

Such philosophical ramifications actually possess empirical validity in the realm of quantum mechanics. The profundity of consciousness is merely the result of the fact that each individual lives in his or her own reality. It is common to assert to a relatively unknowing person on the subject—often to elicit humor—that “all of this may be a dream” (i.e., that the encountered people, places, objects, ideas, and perhaps even the entire life of the respective individual may be artificial constructions of his or her mind). Indeed, when you read this sentence, how do you know that anyone else reads the same words, or even has any conception of a “word”? The mechanics of human vision notwithstanding, your superposition collapse may very well differ from that of the person next to you…

But What About Animals?

Even if one accepts the notion of human consciousness in the context of nature, he or she may rightfully ask whether intelligent and quasi-intelligent animal life exhibits the same relationship to quantum mechanics. That is, can dogs induce decoherence?

Although very few quantum physicists—and by extension, quantum philosophers—have actually investigated the inquiry, most will succinctly answer “yes.” Regardless of how the quality of their senses (sight, smell, hearing, taste, etc.) compare to ours, conscious animals—even if incapable of critical thinking—are observers and thus should be enablers of an object’s reversion into a distinct configuration.

However, just as one human’s superposition collapse and sense of reality is unique, so too is an animal’s sense of reality a mere projection of its own mind. When an animal witnesses an event away from a human, the event occurs as observed only in the mind of the animal. A separate observation from a separate entity (e.g., the external human) yields a separate reality for that entity. Thus, human and animal consciousness, the means of constituting superposition collapse, may be one and the same: a superposition collapse occurs upon an external observation by a conscious entity, with the nature of the decoherence unique to the individual (i.e., not to the species).

Entangled Minds

A uniquely human application to quantum mechanics that is often derided as pseudoscience yet has gained traction with various studies is the idea of entanglement of human minds. Recall that entanglement stipulates that the observation of one particle’s state instantly conveys the state of the entangled counterpart, even if they are separated by millions of lightyears. The idea of human mind entanglement is most notably examined in Dean Radin’s book Entangled Minds.

Image Courtesy of Amazon

Radin puts forth empirical evidence based on several observational studies and surveys that suggests that certain people exhibit behaviors such as:

• Clairvoyance (sensing ongoing events without actually observing them)
• Precognition (foresight; a sense of the future)
• Post-diction (retroactive clairvoyance)
• Telepathy
• Telekinesis

Radin qualifies that such behaviors, if verified, primarily occur among loved ones and relatives. He gives an example of a mother suddenly sensing that “something had happened” to her son as he was killed in combat in the Middle East. He also cites similar instances of one having a premonition that something will happen to a friend or family member if he or she takes a particular course of action.

Although the research is still fledgling and contingent upon parapsychology, Radin suggests that all people to whom one closely associates are subtly or notably connected to that person more deeply than through DNA or mutual affection. Radin, among other physicists, asserts that just as humans may be purveyors of quantum superposition and decoherence, so too may they be entangled through their minds.

Indeed, quantum mechanics has evolved from the successor to relativity to a new branch of neurology. Whatever the future holds for the science, it is certainly uncertain, and it can only be realized by a superposition collapse epitomized in further human (and animal) research and investigation. Will we ever fully come to terms with quantum mechanics? Perhaps, in the ironic words of quantum mechanics skeptic Albert Einstein, it will forever remain elusive and “spooky.”

Why Quantum Computing?

In modern society, digital computers are so pervasive that humans often take for granted the existence of alternative technologies. Moreover, people disregard their shortcomings or areas of improvement to convince themselves that the indubitably dominant paradigm in information processing is permanently in place and increasing in ability ad infinitum.

The pioneer voice of the latter sentiment was Intel co-founder Gordon Moore, who in 1965 published his eponymous law. Moore’s Law states that the computing power of an integrated circuit should double every 18-24 months, and for over 50 years it has remarkably held true.

Courtesy of Forbes

With the turn of the decade less than two months out, however, many theorists have predicted Moore’s Law to expire any time. That is, integrated circuits will soon reach their limits in terms of efficiency, size, and computing power. With the ever-growing threats to security and human demands for complex tasks certainly not reaching their limits, researchers have been exploring a new form of computing to render the infinitely ubiquitous yet finitely reliable digital computer merely another “thing of the past.”

Particularly, various technology firms have been investing in the emergent quantum computing as the means of extending Moore’s Law. Born out of a 1985 paper by Richard Feynman and perpetuated by subtle breakthroughs, quantum computing is as mind-boggling as the system of physics upon which it is based, both in its stipulations and ramifications.

Theory

In classical computing, information is expressed in bits, manifested as series of electrical signals with either high (1) or low (0) voltages. Processing speed is limited by the flow of electricity through the circuitry of the device, specifically in the “von Neumann bottleneck” induced by the delay in synchronizing all components. Moreover, while only semiconductors (specifically silicon) have the right properties to comprise digital computers, they tend to dissipate a great deal of free energy and can only fit so many circuit components before quantum effects (in terms of electron interaction) begin to sabotage the system. This is the precise reason for the stagnation of Moore’s Law; fitting more components warrants a regressive increase in device size after decades of reducing computers from filling entire command centers to fitting in one’s hand.

Courtesy of ThomasNet

Instead of relying on electricity flow, quantum computers render atoms themselves the fundamental units of information. The qubit is defined as an entangled atom in a superposition, not distinctly representing either “1” or “0” like an ordinary bit, but having a nonzero probability of taking on a particular state. That is, knowledge of one atom’s state immediately conveys knowledge of the paired atom’s state, and such atoms can be set up in a circuit-like system similar to that comprised by electrical circuits, but one that is conducive to instantaneous information processing.

The precise behavior of the qubit, just like quantum mechanics itself, is governed by linear algebra and applied probability, both mathematically rigorous and beyond the scope of this overview. It is important to note, however, that the probabilistic states of the qubits are manifested through electron spin; the exact probability associated with a “spin” superposition governs the behavior (and thus applicability) of the respective qubit. As emphasized in the entanglement post (“Spooky Action at a Distance”), two entangled atoms essentially “communicate” with each other by mutually revealing each other’s state upon the observation of one. This property eliminates any latency, or delay for synchronization, in a quantum computer, exponentially increasing both power and efficiency.

Courtesy of Renaissance Universal

Implementation

The previous posts, while warranting the existence of quantum computing, also stipulated the extraordinarily delicate conditions that must exist for superposition and entanglement to be physically realized. Feynman acknowledged this very setback when he proposed the technology in his paper “Quantum Mechanical Computers.” Specifically, the pairs of electrons must exhibit almost no interaction with their immediate surroundings, so imperfectly resistive semiconductors are ineffective. Rather, current quantum devices employ superconductors, the sub-zero temperatures of which allow for the entangled pairs to exist freely. Because superconductors themselves comprise a fledgling paradigm in the realm of electrical systems, primitive quantum computers, much like their classical counterparts of the 1950s, are notoriously bulky and impractical outside a laboratory:

Courtesy of CNet

As complex as Google’s quasi-experimental machine may appear, it only consists of 72 qubits, compared with the gigabytes and terabytes available for memory and storage on modern digital computers. Based on the principles of entanglement and superposition, however, even a modest 72 qubits should be enough to speed up all classical computing processes enormously…at least in theory. It remains the responsibility of theorists to actually develop quantum algorithms that are more efficient that their classical analogues. Google’s recent claim to have achieved “quantum supremacy” with the pictured machine applies only to one particular algorithm, so it embodies only a minute degree of progress. Procedures currently being explored include the Fourier-based Shor’s Algorithm, which promises perfect cryptography and cryptanalysis (and no shortage of civil unrest) if realized in a practical quantum computer. Such ramifications of quantum computing are outlined beyond this technically broad overview in my Rhetoric and Civic Life posts.

Despite the research and associated breakthroughs, quantum computing remains primarily a “thing of the future.” What is, has always been, and will always be an application of quantum mechanics, however, is its association with consciousness and the profound Anthropic implication that humans may indeed be special creatures and the products of a higher design.

It is common knowledge that no information can travel faster than light. Einstein’s Special Relativity has become so ingrained in the minds of the public that contrary suggestions are often met with ridicule. However, both mathematics and experimentation have confirmed the existence of a phenomenon that seems to ridicule Einstein: quantum entanglement.

Electron Spin

In each of the electron clouds around the nucleus (orbitals) described previously, a maximum of two electrons can exist—i.e., with a probability of residing in a position that cannot be pinpointed exactly. Each electron in an orbital must have the opposite spin (denoted “up” or “down”) of its counterpart. The idea of electron spin is not conducive of physical rotation but rather the direction of the magnetic dipole moment of the electron. Elements with several unpaired electrons (and thus the dominance of one dipole direction) include iron and cobalt, rendering them magnetic in nature.

Courtesy of Quora

For any two electrons with a high probability of occupying a specific orbital, the Uncertainty Principle precludes knowledge of their position and momentum; however, knowledge of one electron’s spin immediately deduces knowledge of the other, implied by the Pauli Exclusion Principle.

Entanglement at a Distance

Now imagine a pair of distinct electrons not bound to any particular nucleus. By applying radiation to the electrons simultaneously (e.g., shooting them with a single laser beam), their spins are rendered into a superposition. As long as there is no external observer present during the application of radiation and subsequent separation of the electrons, each particle exists in a probabilistic spin of “up” and “down” simultaneously.

Through electrostatic repulsion and other separation techniques, the electrons are separated a substantial distance, far greater than the radius of any atom. Still having not read the states (spins) of the electrons, an experimenter applies more radiation to one of the electrons and notices that the other electron exhibits the exact same behavior, regardless of its separation distance. The two electrons are thus entangled: effects on one instantaneously induce effects on the other.

The experimenter proceeds to measure the spin of one electron, collapsing the superposition described by the electron’s wavefunction. Remarkably, the Pauli Exclusion Principle dictating opposite spins in a pair holds for entangled particles not bound by an orbital, so knowledge of one electron’s spin immediately conveys knowledge of the other’s. It is as if the information is conveyed at an infinite rate—id est, faster than light.

Courtesy of Universe Review

Implications

Time Travel

While quantum entanglement may threaten the veracity of a component of Einstein’s Special Relativity, his equations do acknowledge faster-than-light travel as a means of traveling backwards through time, due primarily to the idea of the speed of light defining “the present.” Special Relativity also states, however, that attaining a speed equal to or greater than that of light would require infinite energy, for mass approaches infinity as velocity converges to the speed of light. Despite the experimental veracity of information seemingly traveling faster than light, “information” is abstract and massless, so energy remains conserved. Another challenge to the “time travel” idea is that entanglement seems to apply only to subatomic particles, and even electrons are sensitive to separation (only massless photons exhibit perfect entanglement).

Teleportation

Faster-than-light travel into the past is contingent upon instantaneous travel over distance—i.e., teleportation. Researchers have been studying quantum teleportation to address the aforementioned objection regarding macroscopic objects’ inability to entangle. To achieve direct teleportation with an object—e.g., a human being—one must somehow entangle every subatomic particle comprising the object with an exact pattern of particles in the desired location such that the object exhibits a superposition that probabilistically upon observation collapses into the desired “point B” position—i.e., every particle must individually collapse into the wanted position and manifest itself as a component of the object itself. Not only is such an aggregate probability beyond any human conception; it is not entirely clear how the particles would become entangled in the first place. Purpose is defeated if the particles must be relatively close during the actual process (e.g., applying radiation simultaneously).

Quantum Computing

In contrast with the ideas above, quantum computing is certainly feasible and has been practically (albeit primitively) realized. A traditional computer incorporates low and high electrical signals (bits) to convey information in processing and storing. Computing speed and power is limited by the distance between different components and the relatively low speed of electrons through the circuits.

Qubits (quantum bits), on the other hand, allow instantaneous communication among circuit components and networks due to selective entanglement. The precise ramifications of such instantaneous communication will be discussed in the next post.

Courtesy of CNet

Refinement of the Bohr Model of the Atom

Neils Bohr’s model of the atom as a set of electrons “orbiting” the nucleus held for little over a decade after he first proposed it in 1913. The main premise behind the model was the existence of discrete energy levels occupied by electrons; energy is emitted when electrons “step down,” or move closer to the nucleus, and energy is absorbed when electrons move farther away from it.

Courtesy of Wikimedia

Despite conforming to experimentation with hydrogen, the Bohr model broke down for heavier elements such as lithium, beryllium, and oxygen. With a larger and more attractive nucleus, electrons in motion should emit energy to the extent of their collapse into the positively charged nucleus. Additionally, electron positions were found to be more complex than can be described by mere spherical orbits. It seemed as if an observer could never know with certainty where the electron is. Enter physicists Erwin Schrödinger (Austria) and Werner Heisenberg (Germany).

Electron Superposition

In in 1926, Schrödinger shocked even Einstein with a new atomic model has remained the standard for over 90 years yet defies all conventional knowledge about the nature of “reality.” Schrödinger postulated that discrete energy levels did indeed surround the nucleus, but that they took the form of electron “clouds” (known as orbitals) where electrons have a certain probability of being observed. In other words, an electron does not have an absolute position able to be characterized by spacetime coordinates; it is instead in a probabilistic superposition described by the electron’s wavefunction. Only when the electron is observed (which will be shortly demonstrated as a farce) does it theoretically collapse into a definite position in space.

Courtesy of Northwestern University

To the less scientifically adept, the concept of superposition is best analogized with Schrödinger’s seemingly bizarre but entirely plausible thought experiment: Schrödinger’s Cat.

The premise of the experiment involves a cat inside a closed box—i.e., not visible to any observer. There is a vial of poison that, if broken, kills the cat. Whether or not the vial breaks is governed by radioactive decay—a process based solely on probability, perhaps manifested as a Geiger Counter triggering a hammer. The question for an oblivious outsider is, ‘Is the cat dead or alive?’ One cannot settle on one configuration or the other because it is governed by uncertain, probabilistic laws, the results of which have not yet been observed. Schrödinger reasoned that the only logical conclusion is that the cat is both dead and alive, existing in a precarious superposition of life and death, before one opens the box to observe whether or not the Geiger counter has been triggered, whereby the superposition collapses into a single, deterministic state.

Courtesy of Wikimedia

It was previously mentioned that such determinism with respect to electrons was a “farce.” Schrödinger and a number of other quantum physicists theorized that it was impossible to know the precise position and momentum (product of mass and velocity) of an electron simultaneously. The more certain one became about the position, the less certain he became about the momentum, and vice versa. Werner Heisenberg quantified this with his Uncertainty Principle, which implies that knowing the position of an electron within 1 Angstrom (10^-10 m) offsets certainty of its speed by nearly 600,000 m/s. Even motion, as it was discovered, is probabilistic.

Courtesy of HowStuffWorks

As exemplified in the image above, an electron—having nonzero mass—has properties of both a particle and a wave. From the previous post, it was maintained that such a duality also holds for light. Because of the duality, both light and electrons exhibit quantum superposition, with knowledge of position and momentum never certain. However, the superposition phenomenon is not limited to the realm of massless and near-zero mass components of nature: it is exhibited by everything.

De Broglie Wavelengths and the Fall of Determinism

In 1924, French physicist Louis de Broglie published his PhD thesis in which he postulated the quantification of an electron’s wavelength according to the following relationship:

Courtesy of Wikimedia

That is, the wavelength of an electron is inversely proportional to its momentum (h is Planck’s constant). After a pair of experiments confirmed de Broglie’s hypothesis, it was wondered, ‘If an electron exhibits de Broglie wavelength (and thus quantum superposition), then why can’t all matter be associated with a wavelength?’ In fact, the de Broglie wavelength is applicable to everything: protons, baseballs, people, planets, stars, etc.

At rest, a person has zero momentum and thus an infinite de Broglie wavelength, meaning that he acts only as a particle and exhibits no quantum superposition—i.e., his position is absolute. However, when he has nonzero momentum (say, when he is running), he has a finite wavelength and thus possesses properties of both a wave and a particle. At this state, it is impossible to know the runner’s exact position and velocity simultaneously. In fact, when the runner is not being observed with the senses of another conscious being, he exists in a superposition of residing everywhere in spacetime and being both dead and alive! Only when he is observed does the superposition collapse into a quasi-definite position (“quasi” because of the uncertainty principle).

Of course, because of the enormous mass of the runner (and all macroscopic objects) compared with an electron (9.11 x 10^-31 kg), the probabilities associated with his wavefunction are almost entirely skewed toward what we would expect. That is, it would take trillions upon trillions of times longer than the lifespan of the universe for the runner’s superposition to collapse such that he instantaneously tunnels to another planet, but it is entirely possible and has been warranted by experimentation.

Regarding his instantaneous teleportation to another planet, one may wonder how this would hold under Einstein’s special relativity, which sets the speed limit of the universe at 3 x 10^8 m/s, the speed of light. As we shall see in the next post, quantum mechanics may indeed threaten to overthrow relativity theory, which is what prompted Einstein to deride quantum mechanics, specifically quantum entanglement, as “spooky action-at-a-distance” and (rightfully so) at odds with all conceptions of nature.

Think of the most outlandish science fiction ideas ever pursued. Certainly, the classic time travel and teleportation stories, with their share of plot twists and paradoxes, come to mind. One may also conjure up a universe in which information can travel faster than light. Bringing in the notion of consciousness, an author may stipulate that a person knows only what he observes and that anything else is uncertain. How about the existence of an infinity of universes, each with countless worlds very different from, very similar to, and perhaps even identical to our own. Until the last century, ideas as inconceivable as these comprised nothing more than the mere fictional domains of sci-fi authors and storytellers. Not only was it difficult to imagine reality behaving in this manner; no one could imagine it. With the advent of quantum mechanics, however, humans learned that reality (rather, each of their own realities) was not at all orderly and deterministic, but instead uncertain; chaotic; and much, much stranger than fiction.

From Deterministic to Relativistic

Throughout history, humans have sought to explain physical phenomena both on Earth and beyond. Pre-Classical civilizations attributed facets such as eclipses, Moon phases, weather patterns, and plant growth to the acts of deities. It was undisputed that the Earth was at the absolute center of the universe; retracting from such a belief was blasphemous. There was no concept of a “star” other than a small twinkling unit among thousands in the night sky.

In the 4th century BC, the Classical Greeks became the first to call into mind the empirical basis for supposedly supernatural events and objects. Aristotle, following his predecessors Socrates and Plato, attempted to devise systems of physics and chemistry, in which force was directly proportional to velocity and all of matter was composed of some combination of fire, earth, air, and water.  He also attempted to explain the apparent motion of the planets and stars around the Earth with his system of “epicycles,” in which objects revolved in smaller and smaller circles about a main circle around the Earth. The epicyclic cosmology was later refined by Ptolemy in the 2nd century AD to account for observational imperfections in planetary motions; Ptolemy believed that the planets and stars moved in imperfect ellipses.

A contemporary of Aristotle, Democritus, disputed the tetra-elemental chemistry of Aristotle with his atomic theory. He postulated that all matter was composed of indivisible units he called atomos, Anglicized as “atoms.” Democritus theorized that there were not only four types of atoms, but infinitely many, each of which differed in size, spacing, and identity based on the substance it comprises. However, the majority of hoi polloi preferred Aristotle’s model for its simplicity and macroscopic nature.  Moreover, it—along with his and Ptolemy’s geocentric (Earth-centered) model of the universe—would not be contested for nearly 1400 years.

Following the Middle Ages in Europe; the rise and containment of Islam; and the birth and death of Asian empires and dynasties, there was a re-birth of knowledge, epitomized in the Euro-centric Renaissance. Nicholaus Copernicus (1473-1543) began to call the Classical Greek cosmologies into question. Particularly, he noticed how the so-called “inferior planets” (i.e., Mercury and Venus) were never observed more than 50 degrees away from the Sun, leading him to believe that they were orbiting the Sun instead of the Earth. He was corroborated not even a century later by Galileo Galilei (1564-1642)—often considered the father of modern experimental science. Using his telescopes, Galileo not only confirmed Copernicus’s observations regarding the inferior planets but also discovered objects orbiting planets themselves.

With the geocentric model now empirically replaced by the heliocentric (Sun-centered) model, it was time to develop a new mathematics. Johannes Kepler (1571-1630) formulated three laws of planetary motion to explain their elliptical orbits about the Sun. Isaac Newton extrapolated and generalized these laws to momentously assert that all of the universe is governed by one physics independent of location. Developing his three laws of motion and—along with rival Gottfried Leibniz—a mathematics of change known a calculus, Newton constructed a deterministic model of space in which motion was caused by intangible “forces” including gravity and friction. He theorized that all objects with mass possessed their own “gravitational fields” that extended infinitely in all directions and attracted all other objects to it, the force of attraction being proportional to the inverse square of the separation distance.

With a supposedly accurate model of the universe now in place, the nature of the composition of matter came into question over two millennia since Democritus. The English chemist John Dalton refined Democritus’s theory so that each type of atom is associated with a unique element. The structure of the atom came into light with experiments by Ernest Rutherford, J.J. Thompson, and Niels Bohr that resulted in a picture analogous to a solar system, with negatively charged electrons orbiting a positively charged nucleus:

Courtesy of InfoWorld 

Meanwhile, on the macroscopic level, the veracity of Newtonian mechanics was called into question with a series of four modest 1905 papers by a young German clerk named Albert Einstein. Through multivariable calculus and linear algebra, Einstein theorized that space and time were not separate entities but rather one interwoven four-dimensional “spacetime” in which gravity is not due to intangible “forces” but rather the warping of the spacetime fabric by mass. Newton’s laws fit everyday observation very well but failed to account for the bending of light by a star, observed by Arthur Eddington during a total solar eclipse through Africa. Einstein also postulated that the speed of light is both constant and the speed limit of the universe, the former of which was corroborated by the Michelson-Morley Experiment in Cleveland, Ohio. His theories of general and special relativity also defined time based on the speed of light; id est, since light travels more slowly in escaping a large gravitational warp of spacetime, time also passes by more slowly in such a warp.

Courtesy of Discover Magazine Blogs

From Relativistic to Uncertain

Nearly all relevant experimentation has bolstered Einstein’s relativity to the extent of it becoming physical law. Just in 2017, his hypothetical “gravitational waves” emanating from an object of changing mass were detected. Regarding waves of light, however, Einstein’s model may very well fall short…fall short, that is, to quantum mechanics.

Through his study of the photoelectric effect (illustrated below), Einstein knew that light possessed properties of a wave, with its speed defined by the product of its wavelength and frequency. The shorter the wavelength of light, the higher it was in energy, and the faster electrons would be expelled from an atom:

Courtesy of Science ABC

However, in studying the opposite phenomenon—blackbody radiation—fellow German physicist Max Planck discovered that light could be emitted from a body only in discrete units, which he called quanta. That is, light was not found to have wavelike (continuous) properties at all in spite of the existing evidence supporting the wave model. How was this paradox to be resolved? We shall see with quantum superposition that light—and everything else in the universe—must be treated as both a wave and a particle, calling everything from the Bohr model of the atom to the known structure of the universe to the philosophical ideas of consciousness and free will into very deep question…

It is apparent from my both my hobbies and discussion topics of interest that my underlying passion is mathematics. Ever since I entered elementary school, the manipulation of numbers and symbols to describe natural phenomena has intrigued me more than most other facets of my life experience. It is therefore fitting that I should consider writing about some aspect of the subject, be it a historical account or a contemporary research into the latest developments of mathematics. I shall now address both ideas with greater specificity.

1. Historical Account

Part of being civically engaged means having a thorough understanding not only of one’s native language, but of the universal language of nature—mathematics. Unfortunately, throughout primary and secondary education (and even into the university level), such an “understanding” is presented as entailing nothing more than rote memorization and methodical, robotic monotony. “Integrate this function”; “Solve for the determinant of that matrix”; “Add these two vectors”; and “Give the smallest positive integer that satisfies these conditions” comprise just a handful of the phrases repeated semester after semester—year after year—in classroom after classroom. Of course, there is meaningful application presented with each concept, but there is little examination into the origins of the methods and ideas that warrant appreciation for their beauty.

What I would do is examine these very origins. I would take a handful of concepts and methods at a time and ask myself, How did this come into being? Was it derived from empirical observation or pure human ingenuity? In doing so, I would encounter (or in many cases, re-encounter) the numerous mathematicians that have inspired me throughout my life—Euler; Gauss; Fibonacci; Euclid; Archimedes; Cantor; Turing; Fermat; Descartes; Lovelace; and Pythagoras, just to name a few. All of these under-appreciated figures deserve over-appreciation for their contributions, which are now taken for granted. Through the investigation, I hope to not only learn or teach something new, but—more profoundly—to move one step closer to answering the age-old question as to whether mathematics is a mere human conception or truly built into the fabric of nature.

2. Contemporary Research

If one is even remotely familiar with mathematical history, he or she will understand the one commonality in the list of mathematicians above: they are all dead. Some of them have been dead for several centuries, at that. A truly famous and influential mathematician still alive today is almost unheard of. Yes, I do have an unquenchable passion for the subject, but I do concede that it is very slow-moving. It is why the Fields Medal—the most prestigious award in the subject—is distributed every four years with a measly $12,000 prize while the Nobel Prize is awarded annually across six subjects with a much more eye-catching $1.1 million in cash. It is why math class continues to emphasize repetition while science classes—even if they do incorporate math—often examine the latest developments in the field. And it is why this very blog may have to be about one of those developments, a subject that I still understand very little but wholeheartedly enjoy explaining to one face of disbelief after another: quantum mechanics.

I shall spare this very audience’s sanity and preconceived sense of understanding for now. Be aware, however, that if I decide to write about quantum mechanics, one will be questioning much more than whether I made the correct choice; he or she will be questioning the very notion of existence.