As if living in 3D isn’t tough enough, we live in 4D! Einstein and his scientists will agree on 4D spacetime of the three spatial dimensions and the dimension of time, but mathematicians like to play with even more dimensions. Despite my brain’s resistance, a talk I had taught me to visual four dimensional shapes. Your turn:

Let’s start with the 3D cube we’re used to. You can see it mentally with its length, width, and height. Now, if you look at a face of the cube, you’ll see a square which only has a length and a width. This means that the 3D (length, width, height) cube has a 2D (length, width) surface. This can be generalized for any shape:

n-dimensional shapes have (n-1)-dimensional surfaces

So, those scary 4D shapes have 3D surfaces. This sounds fine and dandy, but how the heck can you see that when your brain can only visualize in 3 spatial dimensions?

Let’s consider our cube again. If you want to draw a cube, it’ll look something like this:

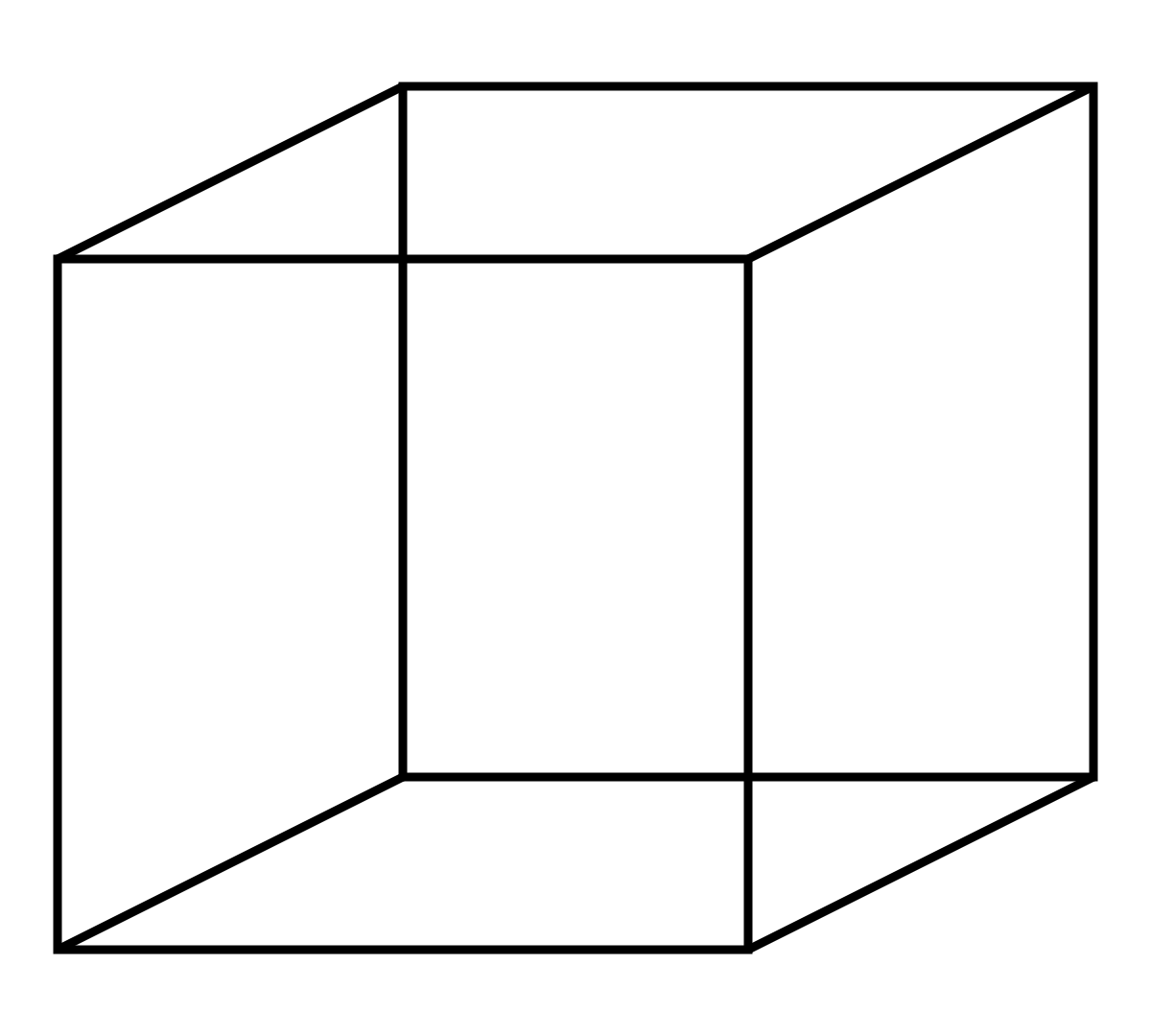
When staring at the picture, you’ll say how that is in fact a cube which is 3-dimensional since you can see what it would look like in real life. But, this is a drawing on the surface of the screen you’re reading this on! Your device is 3D, so the screen surface must be 2D. This drawing of a 3D object in 2D is known as a projection. I projected the 3D object into 2D. This is the key to seeing 4D objects. We physically cannot visualize in 4 spatial dimensions. To accommodate our brains, we can project our 4D object into 3D, using perspective to refer to the extra dimension in the same way as the 2D cube drawing.

Cubes are boring, so let’s look at a 4D pyramid:

The pyramid’s surfaces- the triangles- should be in 3D since the pyramid is 4D. Rather than using our 3 spatial dimensions to visualize the surface, we are projecting the 3D surfaces into 2D. Here’s a drawing of our typical 3D pyramid in the same style as the cube:

So, if this drawing is a 2D projection of the 3D pyramid, we can use it to represent the 3D surface of the 4D pyramid. Those bars that lead into the center of the pyramid create exactly this drawing on every face of the pyramid. Since those drawings are 2D projections, the third spatial dimension allows us to see all 4 faces of the pyramid. in 4D shapes, the 3D surfaces are seen by imagining their 2D projections on the object’s faces.

Once you can separate mathematical dimensions from the physical objects you’re looking at, you too can “see” in 4D.

Stay soupy but in an extra dimension!