Tag Archives: elliptic

Comments on Lecture 22 (today)

Leave a reply

So today we discussed the multiplicative axiom, the last (and most important) of the three “B” axioms that characterize the analytic index.   This axiom says (in its simplest version) that if \(M=X\times Y\) is a product of manifolds and \(a\in K(TX)\), \(b\in K(TY)\), then

\[ \newcommand{\Index}{{\rm Index}} \Index(ab) = \Index(a)\Index(b). \]

In class we discussed the case where the symbols \(a,b\) are represented by differential operators and, following the original paper, we argued using the “double complex” definition of the product on K-theory.  (Jinpeng’s notes, which I’ll post in a moment, give an account of what we said in class.)  Here I’d like to explain how the formalism of \(\newcommand{\Z}{{\mathbb Z}} \Z_2\)-graded operators and vector spaces allows one to make the algebra more concise and conceptual.   (This then becomes part of the formalism that is taken over for Kasparov’s KK-theory.) Continue reading →

Comments for lecture 6

Leave a reply

In this lecture we began the study of the analysis which leads to the Hodge theorem and other key results about elliptic operators.  In subsequent lectures we’ll make use of the work of specialists on pseudodifferential operators (Kohn, Nirenberg, Hormander, Taylor) to prove the estimates we discuss in this lecture.  As Bott said, “If you have an electrical problem, you consult an electrician.  If you have an elliptical problem, you consult an elliptician.”  (Hormander was the go-to elliptician for Atiyah and Bott.)

We began by discussing the Sobolev spaces.   The Sobolev space 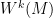W^k(M) on a compact manifold \(M\) is the space of functions whose first \(k\) derivatives (considered as distributions) belong to the Hilbert space \(L^2(M)\).  (In order to avoid an explicit discussion of distribution theory we gave in class an alternative, but equivalent, description which is based on Fourier analysis.)  These form a scale of spaces  (that is, \( W^{k+1}\subseteq W^k\) ) with the following key properties.

  • \( W^{k+s}\subseteq C^k \) whenever \(s> {\frac12}\dim M\);
  • A differential operator of order \(s\) extends to a bounded linear map \(W^{k+s}\to W^k\), for every \(k\);
  • The inclusion \(W^{k+\epsilon}\to W^k \) is a compact linear operator for every \(\epsilon>0\) (Rellich-Kondrakov theorem).

As a result of the second bullet point we can define an operator of order \(\le s\) (not necessarily differential!) to be any linear map on smooth functions that extends to a continuous map \(W^{k+s}\to W^k \) for every \(k\).   Every differential operator of order \(\le s\) is an operator of order \(\le s\), but the converse is of course false.  In particular there exist “operators” of negative order.  That makes the following statement sensible.

Fundamental Elliptic Theorem  If \(D\) is elliptic differential of order \(s\), there exists \(Q\) of order \(-s\) such that

\[ I-DQ = R_1,\quad I-QD = R_2 \]

are smoothing operators (i.e. of order \(-\infty\)).

In the next couple of lectures we will see how the pseudodifferential calculus is used to construct the parametrix \(Q\).   You could read about this in the Kohn-Nirenberg papers (see Atiyah-Bott’s bibliography) or in M. Taylor,Pseudodifferential operators, Chapter II (very terse).

 

Alok’s question

Leave a reply

So, in class today, we were talking about what it means for a (constant coefficient) operator to be elliptic.   If \(D\) is such an operator, of order \(m\), say

\[ D = \sum_{|\alpha|\le m} L_\alpha \frac{\partial^\alpha}{\partial x^\alpha} , \]

then the correct definition of ellipticity is that the principal symbol

\[ \sigma_D^m = \sum_{\alpha = m} L_\alpha \xi^\alpha \]

should be invertible for all \(\xi\neq 0\).   This of course implies that the total symbol (which we just called the symbol)

\[ \sigma_D = \sum_{\alpha \le m} L_\alpha \xi^\alpha \]

is invertible for \(\xi\) sufficiently large, and in class I incautiously stated that the reverse implication is true as well.  Alok correctly questioned this, pointing out that lower order terms could tip a non-invertible principal symbol over into invertibility: a simple explicit example is the symbol

\[ \left(\begin{array}{cc} 1 & 0\\ 0 & 0\end{array}\right) \xi^2 +  \left(\begin{array}{cc} 0 & 0\\ 0 & 1\end{array}\right) \xi\]
which should not be classed as elliptic.  (In my defense, I will say that there is a sense in which it is true that “an operator is elliptic if and only if its total symbol is invertible for large \(\xi\)” – as we will see when we discuss pseudodifferential operators – but the word “invertible” has to be interpreted in a more sophisticated way than mere pointwise invertibility for each \(\xi\) individually.)   Apologies for the confusion here, and thanks to Alok for keeping me on track.