In this lecture we finally got around to defining what a pseudodifferential operator is (at least on 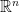.  It is an operator whose distributional kernel is given by an oscillatory integral

\[ k(x,y) = \int e^{i(x-y)\cdot\xi} a(x,y,\xi) d\xi, \]

where the amplitude \(a\) is a function on \( {\mathbb R}^n\times {\mathbb R}^n\times {\mathbb R}^n\) that satisfies estimates of the following form: for each compact \(K\subseteq {\mathbb R}^n \) and for all multi-indices \(\alpha,\beta,\gamma\) there is a constant \(C = C_{K,\alpha,\beta,\gamma}\) such that

\[ | \partial_x^\alpha \partial_y^\beta \partial_\xi^\gamma a(x,y,\xi) | \le C (1+|\xi|)^{m-|\gamma|} \]

where the constant \(m\) is the order of the amplitude.   We saw that the oscillatory integral can be regularized by repeated integration by parts and that it defines a distribution with singularities only along the diagonal which maps \(C^\infty_c({\mathbb R}^n) \) to \(C^\infty({\mathbb R}^n)\) and which also, under some mild support conditions, maps distributions to distributions.

I concluded by stating that one can “quantize” on the left or teh right, in other words one can represent any pseudodifferential operator, modulo smoothing operators, by an amplitude \(p(x,\xi)\) that is independent of \(y\), or by an amplitude \(q(y,\xi)\) that is independent of \(x\).  We’ll develop this idea next time.