Welcome back, readers. The music theory nerd’s paradise continues to expand. Today’s topic: secondary dominants.
We’ve discussed dominant chords in the past. They create tension/instability that can be resolved by moving back to the tonic chord in a given key. The perfect cadence is a standard example of this idea, moving from V to I.

However, in the Western tradition of music, staying confined to the dominant chords found within a single diatonic key (traditionally, the V and vii0) is simply not enough to quench our undying thirst for interesting harmonic material. To remedy this problem, musicians utilize secondary dominants.
To adequately explain this concept, we must look at the Circle of Fourths. What is the circle of Fourths? Here it is:
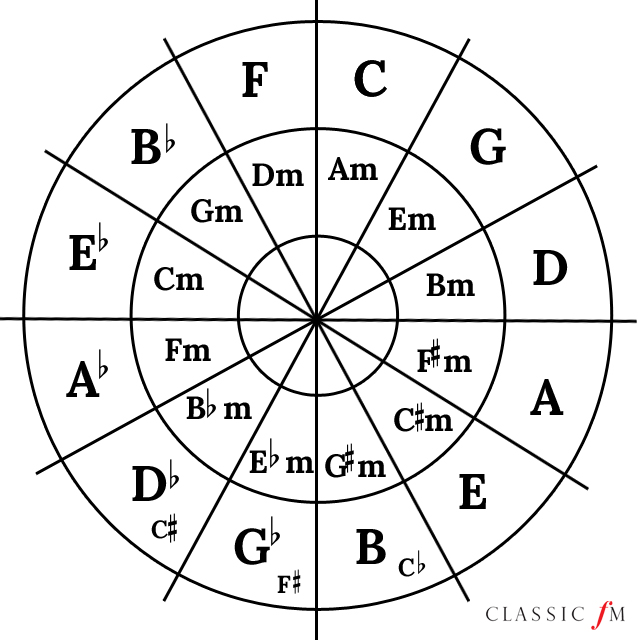
Those of you who are classically trained may be shouting in vigorous protest at your computer screen: “No, no! That’s the Circle of Fifths!” Whether or not this is the case, I invite you to take a closer look.
This image visually represents the twenty-four keys of Western music and how they are related. The major keys are located in the outer rung of the circle, and the minor keys are located in the inner rung of the circle. Each major key’s relative minor key (sharing the same notes) is located within the same “pizza wedge.” The sequence of keys are arranged in a manner such that (1) as one travels clockwise around the circle, one travels a fifth between each key, and (2) as one travels counter-clockwise around the circle, one travels a fourth between each key.

For the purpose of secondary dominants, conceptualizing the circle as the Circle of Fourths is more helpful. To explain why, let’s traverse the circle counterclockwise.
We begin with F, which is the fifth of Bb, the next note in the traversal. This means we can create the perfect V-I cadence F7-Bb. Let’s continue. Next after Bb is Eb. Bb is the fifth of Eb. We notice a pattern–why not make Bb a dominant chord resolving to Eb? Now our progression is F7-Bb7-Eb. We can keep moving counterclockwise around the circle in this manner until we again reach F: F7-Bb7-Eb7-Ab7-…-C7-F
Obviously, such a progression would be excessive, but this harmonic idea is used all the time in music. Take a look at the chords which sit under the titular lyrics of “Make You Feel My Love” by Bob Dylan (D7-G7-C). Or, take a look at the chords of the intro to “Bohemian Rhapsody” by Queen (Bb-C7–F7–Bb-Gm7-Bb7–Eb-Cm7-F7).
Notice how in Bohemian Rhapsody a few ii-V-I’s are thrown into the mix. This is called interpolation, and will be explained in a later post.
Wow, this was really interesting to read, I’ve read many blogs through out this course and I haven’t seen anyone do any topics like music or music composition so this was a fun read. I really enjoyed how you put visuals inside of the blog post to help reader’s follow along, even if they had no idea what it was you were explaining.
I also really appreciated how you gave specific songs that included the notes you were writing about. Bohemian Rhapsody is a great song!!
By going through this blog I can tell how much you love music, and you certainly. know a lot about it. I have played an instrument in the past, I had absolutely no idea about the Circle of Fourths and Fifths, and that link really helped me a lot. This is hugely interesting, and I am looking forward to your post own interpolation.
Wow Ethan, your in-depth knowledge surrounding this topic is so interesting as I had no idea of the specific mechanics that it takes to create a perfect harmony. After reading your blog (and having nearly no prior knowledge on the logistics that go into creating the perfect note) I listened to Bob Dylan’s “Make You Feel My Love”, and Queens’s Bohemian Rapsody and really could appreciate the creation of that “perfect cadence” you mentioned above that is the direct result of trans versing the circle of fourths counterclockwise. I did not entirely understand the concept of interpolation within musical notes; however, I am beyond elated to read about it in the next installation of your blog, Great work!