As a student currently surveying several subjects for further study, I can personally appreciate the life story of the German polymath Gottfried Wilhelm von Leibniz. Though Leibniz is best known for his calculus notation and optimistic philosophy, he also excelled in several other fields. Despite spending much of his life working at jobs unbefitting of his intellectual capacity, Leibniz took every opportunity to expand his knowledge further. When he was supposed to be collecting historical information or conducting diplomatic missions, Leibniz spent his time having mathematical and philosophical discussions with fellow Enlightenment thinkers. He corresponded with over 600 scholars in total during his lifetime and went on to set up academies throughout Europe to encourage interdisciplinary study.

Gottfried Wilhelm von Leibniz pronounced “LIBE-nitz”
Gottfried Leibniz was born in Leipzig (in modern-day Germany) in 1646, during the final years of the destructive Thirty Years’ War. His father, a moral philosophy professor at the University of Leipzig, died when Leibniz was just six years old. However, Leibniz managed to learn large amounts of information from his father’s books and even taught himself Latin and Greek. During that time, he questioned Aristotle’s system of logic and adopted his mother’s Lutheranism.
Leibniz attended the University of Leipzig at age fourteen, where he focused primarily on philosophy. He gained interest in interdisciplinary work when a math professor discussed the potential application of mathematical proofs to fields such as logic and philosophy. Coincidentally, when I expressed my interest in math at a recent Penn State event, someone told me that advanced mathematics and philosophy can merge together. In Leibniz’s case, this revelation led to his idea for a comprehensive scheme of human knowledge.
Though he had built a scholarly reputation and completed his legal studies, the University of Leipzig refused Leibniz a doctorate in law In 1666. Disgruntled, he went to Altdorf and received his doctorate immediately upon submitting his dissertation De Casibus Perplexis. However, he turned down a position at Altdorf and went to Frankfurt for a few years to work for the German statesman Baron Johann Christian von Boyneburg.
Leibniz was a very literary man during his time there, thinking like a Renaissance humanist (such as Desiderius Erasmus). He developed a desire to reconcile the Christian churches, and to that end he often discussed religion with Boyneburg, who was Catholic, and wrote papers about their ideas. Boyneburg also introduced Leibniz to the Archbishop (and prince elector) of Mainz.
The Archbishop conceived of a plan to divert Louis XIV’s attention from the German lands: encourage him to send a religiously motivated expedition into Egypt. Leibniz saw in this a potential for uniting the churches and ultimately traveled to Paris in 1672 to carry out this diplomatic mission. However, this idea prompted far more philosophical and theological thought on the part of Leibniz than practical diplomatic results.
Before travelling to Paris, Leibniz developed the principle of sufficient reason (I know this is important because it came up in quiz bowl yesterday); it essentially states that there is a reason for everything – a cause or justification for the existence of everything that exists and a reason for every event that occurs. He published this and many more ideas in Demonstrationes Catholicae and Hypothesis Physica Nova, both of which held the existence of God as essential to their conclusions.
In Paris, Leibniz similarly focused on developing his ideas; he discussed church reunification with the theologian Antoine Arnauld and studied math and physics under Christiaan Huygens, rapidly increasing his expertise on those subjects. Leibniz was also to go on a diplomatic mission to London, so he made contact with scientists and mathematicians there and became a fellow at the Royal Society of London in 1673. Both Boyneburg and the Archbishop died without Leibniz having made any progress with the diplomatic assignments, and he returned to Paris after the Archbishop’s death.

One of Leibniz’s lengthy correspondences
While in Paris, Leibniz began to develop his calculus. He worked from a geometric perspective, thinking of derivatives as infinitesimal changes; though this way of thinking about calculus is no longer the preferred method, his notation is still used for both derivatives and integrals, as it is far better suited for advanced calculus than Isaac Newton’s.
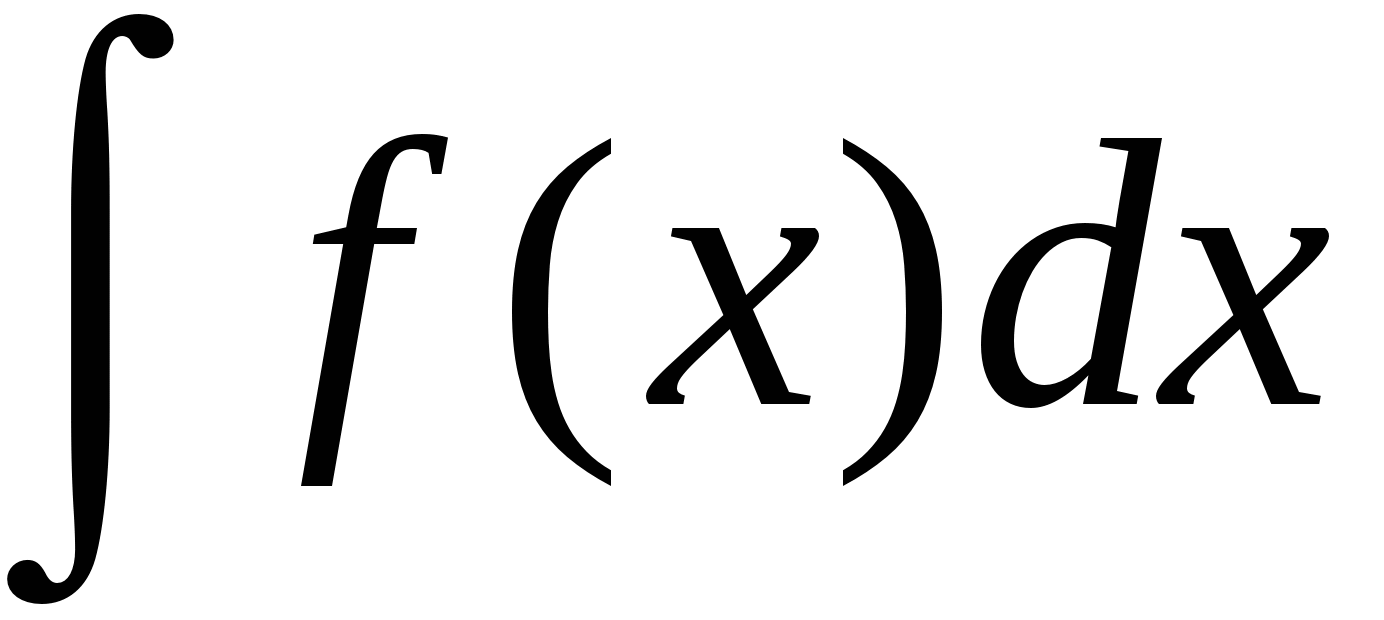
Leibniz notation for an indefinite integral

Leibniz would have been happy to stay in Paris, but the Paris Academy of Arts and Sciences did not extend an invitation to him; apparently the French decided there were already too many foreigners in the Academy. Leibniz was thus forced to leave Paris, moving back to “Germany” to accept a post under the Duke of Hanover. His work was mundane, but he took on a number of ambitious side-projects and used those to study a great many topics.
For example, when he was commissioned to write a history of the Brunswick family, he spent years gathering and publishing archival information about the family; this entailed traveling to Vienna and Florence and talking with fellow scholars, but he never wrote the work that had been commissioned.
He also attempted to engineer a means of draining water from a mine in the Harz mountains using pumps powered by hydroelectric and wind power. These attempts repeatedly failed, but he made interesting geological discoveries in the process and became the first to posit that the Earth was originally molten. However, his pioneering of wind-harnessing technology is disputed.

Design of Leibniz’s plan in the Harz Mountains
During this time, Leibniz also made advances in mathematics, physics, philosophy, and theology. He published his theory of calculus in the mid-1680s, eliciting plagiarism allegations from Newton. Since Newton was the head of the Royal Society of London, he heavily influenced the Society’s investigation; unsurprisingly, it concluded that Leibniz had stolen his theory of calculus from Newton. Later analysis indicates that they invented calculus independently, building on the previous work of mathematicians such as Rene Descartes and Pierre Fermat.
In physics, Leibniz criticized Descartes’s mechanics and studied what are now known as potential energy, kinetic energy, and momentum. However, his perspective was too broad to have an immediate impact in the field. His major work was Dynamica, which was published in 1689.
He also conceived of many essential logical operators, which have been discovered in his working drafts. Though they were not published, his ideas regarding logic were the most important between Aristotle’s in Ancient Greece and George Boole’s in the 1800s.
Leibniz also rediscovered the use of matrices and binary, which were originally invented by Ancient Chinese mathematicians. His use of matrices to solve linear systems of equations paved the way for further work in linear algebra by Carl Friedrich Gauss in the early 1800s. Leibniz’s perfection of the binary number system was also vastly influential. He used it in his calculating machine, which was an improvement over Pascal’s rudimentary adding machine, and binary has been essential to all programming advances since then.

Obligatory ones and zeroes
In philosophy, Leibniz’s published work represented a fraction of his thinking on the subject and was rosier than his actual views, which were more logical and precise. Much of his own thinking dealt with a comprehensive system of human knowledge. Perhaps the romantic tone of his published work is best reflected in Discourse on Metaphysics (1686), in which he argues that the world was created in pre-determined harmony by a benevolent deity, a “best of all possible worlds”.
In Theodicy (1710), Leibniz revisited the dilemma of how bad things can happen in a world created by a benevolent God. This goes back to his principle of sufficient reason, which holds that there is a reason or cause for everything. Personally, I think that this is a faulty premise and led to his more outlandish conclusions, such as the “best of all possible worlds” claim; Voltaire satirized this in his 1759 novel Candide, with the protagonist insisting all is for the best as terrible things happen all around him.

Ever the optimist
Near the end of his life, Leibniz worked to set up academies in Vienna, Dresden, Berlin, and St. Petersburg, cementing his legacy defending multidisciplinary progress. He had the rare distinction of being on the leading edge of the varied disciplines of math, logic, physics, geology, philosophy, history, and theology all at once. Though he is primarily remembered as the target of Voltaire’s satire and as second fiddle to Newton, Leibniz did make important advancements in multiple fields and his life remains a testament to scholarly pursuits.


That was an awesome read, and I love your images. First that hair, and second the caption. Also a lot of super cool info on Leibniz. He probably wasn’t as smart as our calc professor though.