Category Archives: Uncategorized

Note: You will need pencil and paper for this blog.

Is it possible to predict how high the sun rises on a given day? If so, can we find this information for State College, PA?

Consider the Earth during an equinox.

Recall that the sun is directly overhead of the equator at this time. To represent this, draw a circle with a light ray coming from the right pointing towards the center of the circle. Now, assuming the sun’s light rays are parallel to each other (in reality, they are not so because the sun is spherical, but Earth’s distance from the sun mitigates this effect), draw another light ray parallel to the one already drawn that points above the center of the circle. Draw a tangent line where the second light ray strikes the circle’s edge. The angle between the second light ray and tangent line approximates how high the sun rises at that location on the circle’s edge during an equinox. For the sake of mathematical discussion, call this angle θ.

Extend the first light ray to the center of the circle. Using an appropriate radius, connect the location where the second light ray intersects the circle to the center of that circle as well. The angle between these segments is just the location’s latitude. We define that as the angle ϕ.

Now extend the tangent line until it intersects the first light ray. Notice the triangle formed by this extended line, the first light ray, and the radius that connects the center of the circle and intersection of the second light ray with the circle is right because the tangent to a circle at a point is always perpendicular to the radius which connects that point to the circle’s center.

Two of the angles in this triangle are fairly obvious—ϕ and 90°. It can be shown by the alternating interior angle theorem of parallel lines that the third angle is θ. These three angles must add to 180°.

Thus,

θ + ϕ + 90° = 180°

Therefore,

θ = 90° – ϕ

During an equinox at State College (latitude of 40.8°N), we expect the highest solar zenith angle to be 49.2°.

What if we wish to find the maximum solar zenith angle at any time of the year? Using the same methods presented here, I invite you to come up with your own solution.

Consider a spinning ice skater. To increase her rate of rotation, she brings her arms closer to her body. Why does this occur? The answer lies within conservation of angular momentum.

Now you may have seen this concept discussed in your standard mechanics course, like PHYS 211 or AP Physics. You might also recall that the magnitude of angular momentum is the product of angular speed and moment of inertia, where the moment of inertia quantifies the distribution of mass from some fixed rotation axis. Unfortunately, such a nice relationship is not so for most atmospheric phenomenon because air parcels are not solid bodies like those observed in PHYS 211. Only at infinitesimal scales can solid body rotation approximate atmospheric circulation.

Fortunately, Rossby, an atmospheric dynamist, simplified our need to look at infinitesimal scales with the concept of barotropic potential vorticity:

              D[(ζ + f)/h] /Dt = 0 

What each variable means in this equation is not of significant importance to us. For now, just consider ζ to be a measure of spin (where positive values indicate counter-clockwise flow), f to be a positive constant, and h to be height.  The physical interpretation of Rossby’s formula is the following: If a column of air compresses or expands (causes height changes), then the trajectory of that column (its spin) will be distorted.

Now consider a uniform flow of air headed eastward towards a mountain. What happens to the trajectory of the air column as it reaches the peak of the mountain?

  D[(ζ + f)/h] /Dt = 0

  (ζ + f)/h = positive constant 

Notice that, if height decreases, the numerator must decrease to balance the constant. If f is a positive constant, then ζ must be negative to decrease the numerator. Therefore, the column acquires a clockwise spin and moves southward.

So if you ever look at a weather map of wind speeds and directions, take a closer look at the flow before and after winds reach the Rocky Mountains. You may be able to see the dip southward courtesy of angular momentum conservation.

When someone mentions a heat engine, we all picture the familiar steam locomotive, complete with moving wheels, a furnace, smokestacks, and whistle. But what exactly is a heat engine? What does it do?

Thermodynamically speaking, a heat engine is any mechanism used to accumulate mechanical work through both transmutation and transportation of thermal energy. In laymen’s terms, a heat engine takes disorganized energy from molecules in “hot” objects, organizes some of that energy into a usable form (i.e. to move a piston), and dumps excess disorganized energy into “cold” objects. We can represent a heat engine in the following schematic.

T_H is the temperature of the hot reservoir. Q_H is the amount of thermal energy being provided to the engine. W is the usable work coming from the engine. Q_C is the amount of thermal energy leaving the engine. T_C is the temperature of the cold reservoir.

The efficiency of an engine is defined as the ratio between its production of usable work and the amount of thermal energy originally supplied to it. Mathematically, η = W/Q_H. From conservation of energy, we know that the amount of thermal energy supplied to the engine must equal the work produced by that engine in addition to the amount of thermal energy leaving it. In other words, W = Q_H – Q_C. Thus, η = (Q_H – Q_C)/Q_H = 1 – Q_C/Q_H < 1. Consequently, the efficiency of any heat engine will be less than 100%.

With greater knowledge of thermodynamic principles, it can be shown that the maximum efficiency for any heat engine is given by η = 1 – T_C/T_H.

Now consider the troposphere, the layer of air in which our weather occurs. The average temperature across the poles over a given year is about 250K (about -10°F). The average temperature across the tropics over a given year is about 305K (about 90°F). The maximum efficiency of this heat engine to create usable work (i.e. weather) is roughly 18%.

Believe it or not, but even the most severe weather systems are merely a small fraction of an already small percent of usable work permitted in our troposphere. Imagine the weather without the 18% usable energy cap. Pretty scary, huh?

Over the last two weeks, we have been discussing applications of atmospheric motion, from an introduction to the forces acting on an air parcel to an illustration of their net macroscopic contributions, i.e. the Hadley Cell. Today will be similar in content, but our main focus will be dispelling a popular belief about how water spins in our toilet bowls.

Recall the idea of geostrophic flow: Pressure gradient force balances the Coriolis force, where the pressure gradient force points in the direction of lowest pressure and the Coriolis force, in the Northern hemisphere, acts to the right of an air parcel’s velocity.

Now consider an area of low pressure at 1004mb over Penn State. Air parcels in all directions will be pulled towards us by the pressure gradient force, right? Do they ever make it to us? Theoretically, if geostrophic balance holds, they will not. (In the real world, where friction exists, geostrophic balance breaks down, and therefore, the parcels will make it Penn State.) Why then do the parcels not make it to Penn State assuming geostrophic conditions? The answer is simple: The Coriolis force directs the parcels to the right of their velocities.

To get an idea of the net trajectory of all these are parcels, consider four of them: One coming from the south, one coming from the east, one coming from the north, and one coming from the west.  The parcel coming from the south will be directed to its right, which will be to the east. The parcel coming from the east will be directed to its right, which will be to the north. The parcel coming from the north will be directed to its right, which will be to the west. The parcel coming from the west will be directed to its right, which will be to the south. The resulting configuration should not be too surprising.

We have all been taught or learned from experience that low pressure systems have a counter-clockwise spin in the northern hemisphere.

I encourage you to explain to yourself why low pressure systems have a clockwise spin in the southern hemisphere given that the Coriolis force acts to the left of an air parcel’s velocity.

Now, how does this relate to toilet bowls?

How many times have you heard that, in the southern hemisphere, water in toilet bowls spin clockwise, opposite the direction observed in the northern hemisphere? Is this observation correct?

The answer is no. For toilet bowls to spin clockwise, as we have demonstrated with weather systems, the Coriolis force must play a role in a force balance with the pressure gradient occurring within the toilet bowl. The Coriolis force, as mentioned two weeks ago, only has significant impacts for large scale phenomena on Earth. Therefore, the rotation of the water in a toilet bowl is caused not through geostrophic balance, but by applying a mechanical torque on the water. These torques are byproducts of manufacturers’ toilet designs; nature does not provide them.

Hence, when you hear about this observation, keep in mind it is a myth designed for the unknowing northern hemisphere traveler; water in toilet bowls from the southern hemisphere can and do spin the same direction as our toilet bowl water.

Because of Earth’s axial tilt, curvature, and rotation, we tend to have a surplus of energy near the equator and a deficit near the poles. Faced with this stark inequality, our atmosphere plays the part of Robin Hood—taking from the energy surplus and giving to the energy deficit. This process of transferring energy from the equator poleward is known by atmospheric scientists as the general circulation of the troposphere. We will see in upcoming blogs that our atmosphere, even with its greatest attempts to reach equality, can never quite balance this energy budget occurring on Earth’s surface.

To describe general circulation, we are going to follow an air parcel as it flows from the equator northward.

Our parcel’s journey begins at the equator, where energy is “laying around” in large quantities. Through absorption of this extra energy, the parcel increases its temperature and, therefore, decreases its density. At some point, our parcel’s density becomes less than the environment around it, and so it rises to the top of the troposphere. An example analogous to this movement would be when you release an inflatable ball from the bottom of a swimming pool.

When our parcel reaches the top of the troposphere, called the tropopause, it stops rising and is forced instead to move either north or south. A nice way to think about this transaction is by considering a bottle of toothpaste. For instance, if you cap your toothpaste bottle, then, when you go to squeeze your toothpaste upwards, it will actually be forced by the cap to move horizontally. The same concept occurs in the tropopause. Suffice it to say that, in this case, our parcel chooses north as its intended path of travel.

We know from last blog what happens to parcels traveling north from the equator. They must obey geostrophic flow.

Therefore, while initially moving northward, our parcel is continuously reflected ninety degrees to its right by the Coriolis force until it is moving perfectly eastward. In doing so, the parcel never makes it to the north pole, its intended destination. In fact, calculations can show that it gets stuck around 30°N.

Many air parcels “pile up” at this 30°N location, creating a stream of air that encircles the earth below it. Intentionally, we call this pile up of moving air the subtropical jet stream. In central Pennsylvania, we usually do not experience much from this stream of air, and if we do, it occurs during the summer months, when the subtropical jet stream is slightly north of 30°N. Most of the time, we are victims of what is called the mid-latitude jet stream, a structure much more difficult to understand that I may take about in future blogs.

As you might imagine, things can get pretty heavy in the subtropical jet stream when more and more air parcels enter it, and so the air eventually sinks due to gravitational forces. Not unlike what happens at the tropopause when air rises, air that sinks towards the surface, too, has a choice to move north or south. This time, let us say for the sake of discussion that the air parcel chooses to move south, back to the equator.

Ignoring frictional forces, we have yet another case of geostrophic flow. Instead of moving initially northward, however, our parcel is moving southward. Therefore, when our air parcel is deflected continuously to its right, the direction of travel becomes an easterly wind (wind that flows from the east to the west). This easterly flow is known as the trade winds, famous for helping Europeans sail to the Americas during the times of colonialism.

As you can see, once the parcel reaches the equator (which it will just barely do because of the Coriolis deflection), the process begins anew. We call this cycle the Hadley Cell; it is the fundamental description of average atmospheric motion in the tropics. (To understand what happens above our heads, in the mid-lattitudes, requires more sophistication but, in general, follows similar principles displayed in the Hadley Cell.)

An illustration of the Hadley Cell can be shown below.

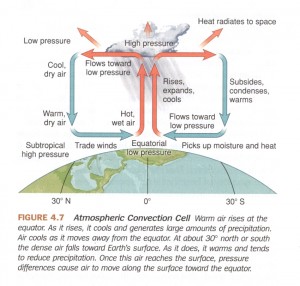
Fundamentally, there are three real forces that can act on an air parcel: Gravity, friction, and pressure-gradient. Gravity and friction probably make the most intuitive sense to you by now because they are heavily stressed in high school physics. As a brief refresher, the force of gravity tends to pull objects, in this case air parcels, towards the center of the Earth, and friction tends to act in the opposite direction of an air parcels’ velocity.

Many times, we only care about horizontal transport of air parcels in the troposphere, and so, gravity is omitted in calculations because it acts perpendicular to the surface of Earth. In a similar manner, since we often only care about this horizontal transport in the upper Troposphere, where interactions with a rugged surface are not common, we also neglect friction. That leaves us with only the pressure-gradient force to worry about.

The concept of pressure-gradient force is actually quite simple. Imagine a glass tank consisting of two equally sized chambers separated by a wall. If we then fill the two chambers with unequal amounts of water (i.e. one water level is higher than the other), then we can deduce that the water pressure at the bottom of the chamber with more water in it will be higher than that of the chamber with less water in it. If we now remove the wall between the chambers, what happens? The chamber with more water flows into the chamber with less water until the chambers have an equal water level. Another way of saying this would be that the chamber with higher water pressure flowed towards the chamber with lower water pressure until the water pressures in each chamber reached an equilibrium.  This flow from high to low pressure is called the pressure-gradient force.

Here is the same concept of pressure-gradient force presented visually by an arrow.

You would think that, after mastering how to describe these three fundamental forces mathematically, we could explain all phenomena in meteorology. That, however, would be incorrect. We actually require two additional apparent (“fictitious”) forces to enhance our understanding. These correction forces take into account that the Earth is spherical and, more importantly, rotating.

One apparent force is called the Coriolis force. (Perhaps the name sounds familiar to you in your previous Earth science classes. I may go into more details about it in a later blog.) For now, just note that the Coriolis force pulls air parcels ninety degrees to the right of their velocities in the northern hemisphere, as shown below.

The other apparent force is called the centrifugal force. We’ve all experienced its effects when we turn the wheel of our cars. Everything, including ourselves, seems to push away from the center of the circle in which we’re traveling. The same thing is true of air parcels rotating with Earth: They are being pushed away from the centers of the circles in which they are rotating. (For those of you who enjoy physics, the centrifugal force has the same magnitude as the centripetal force, but opposite direction.)

One nice attribute of apparent forces is that they contribute very little when describing motions for small-scale weather systems (i.e. lake-effect snow, sea breezes, tornadoes, etc.). However, when describing the entire motion of the atmosphere and of large-scale weather systems, the Coriolis force, in particular, matters quite a bit. (The centrifugal force, as a whole, is small no matter the size of the system we consider on Earth. Therefore, it is often neglected altogether.)

Let’s take an example of all the information we’ve discovered.

Let’s say that the pressure above the equator is 908mb and the pressure above 30°N is 900mb. If an air parcel is initially at rest above the equator, what will its trajectory appear to look like from an observer on Earth as it moves from higher pressure to lower pressure? (Note: Since we are not moving vertically and we are high up in the troposphere, we can neglect gravity and friction. Thus, the only two forces that we have to consider will be the pressure-gradient and Coriolis forces.)

I think we can all agree that the parcel of air will be attracted to lower pressure at 30°N and, therefore, move northward initially. However, recall that the Coriolis force pulls parcels ninety degrees to the right of their velocities in the northern hemisphere. Therefore, what was once a northerly track becomes a northeasterly track, and what was once a northeasterly track becomes more and more easterly. When a parcel moves due east, notice the pressure gradient force and Coriolis force will balance. (The pressure-gradient force will be pulling the parcel upwards, and the Coriolis force will be pulling the parcel downwards.) An illustration of this force balance is shown below.

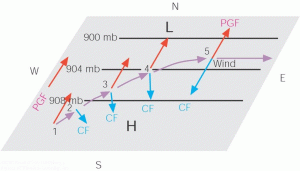
We call this balance between pressure-gradient force and Coriolis force geostrophic flow. It is a fundamental identity, not necessarily a catch-all definition, of how air moves in the troposphere. Nonetheless, we will exploit this special-case situation to describe the “general circulation” of the troposphere, how air moves on average over the entire globe, next time.

So, to summarize, air parcels are generally set into motion by pressure-gradient forces, though friction or gravity could also play a role. These motions are then distorted by the fact that we are rotating on a spherical Earth, and so forces like Coriolis are needed to show how air parcels behave once initially set in motion. A fundamental outcome of the net-effect of all these forces is called geostrophic flow, which essentially states that air parcels will stabilize their directions when the pressure-gradient force is in balance with the Coriolis force. In general, air does not always move in this manner, but it is a decent first approximation.

Many of us have studied at one time that pressure in the atmosphere is greatest towards the surface of the Earth and significantly less the further we distance ourselves from that surface. If some of us have forgotten this concept, then we might have experienced it when traveling on a commercial airline or during a car ride through the mountains: Our ears, accustom to sea surface pressure, seem to “pop” when exposed to the lower pressures surrounding us at higher altitudes.

Below is a common graph of average altitude as a function of pressure for the atmosphere.

Here are a few notes about the graph that are important to know.

1. As pressure decreases, altitude increases. Notice the graph is not linear. (The graph is not a line.)
2. The height of Mt. Everest is about equal to the average height of the troposphere, the layer of air in which we reside that I talked about last week. (Remember I said something to the effect that about eighty percent of the atmosphere falls in the troposphere. Take a look at where Mt. Everest falls in terms of percentage of atmospheric pressure.)

Question:

How do we know this graph is an accurate representation of the atmosphere?

Answer:

With a bit of high school physics and a smidge of calculus, we can explain why the atmosphere behaves in this manner.

Consider a rectangular slab of air. Fundamentally, there are three forces acting on this slab—gravity (F_G), the force of air below the slab (F_B), and the force of air above the slab (F_A). Gravity and the air above the slab push downwards. The air below the slab pushes upwards.

If we assume that the slab of air is not moving vertically or is moving at a constant velocity vertically, then (by Newton’s Second Law) the net force on the slab must be zero.

– F_G – F_A + F_B = 0               (1)

If we assume that the slab of air is close to Earth, the force of gravity is given by F_G = mg, where m is the mass of the slab and g is the acceleration due to gravity (9.80m/s²). Both forces due to air above and below the slab can be rewritten as P_AA and P_BA, where P_A is the pressure at the top of the slab, P_B is the pressure at the bottom of the slab, and A is the cross-sectional area of the rectangular slab.

– mg – P_AA + P_BA = 0       (2)

Doing some algebra, we can come up with the following relationship. (∆ means “change in.”)

∆P = P_B – P_A = – mg/A    (3)

Recall that density ρ is defined as mass m per unit volume V. Using this definition, let us make a substitution for the mass of the slab in the equation.

∆P = – (ρV)g/A                  (4)

Volume is defined as the product of the rectangular slab’s length, width, and height. Area is defined as the product of length and width of the slab’s horizontal faces. Notice that dividing volume and area yields the height of the slab, which we will call ∆z.

∆P = – ρg∆z                        (5)

If we “squeeze” our rectangular slab vertically so that its height is infinitesimally small, we would expect that the change in pressure from the bottom to the top of the slab would also be infinitesimally small. (We assume that the density of the air slab and the acceleration due to gravity remain constant when we make this compression.) To distinguish this infinitesimal change in variables P and z, we will use the notation ∂P and ∂x rather than ∆P and ∆z. (If you want to impress your friends, the resulting equation is called hydrostatic balance.)

∂P = – ρg∂z                         (6)

Notice that, if we accumulate all the changes in pressure by adding up all the ∂P for all the rectangular air slabs that make up the atmosphere, we can derive an equation for pressure in terms of altitude. (We are going to integrate this expression, in other words.) Before we do this, I want to make a quick note that density is not necessarily constant when we do this summation. In fact, density depends on pressure according to the ideal gas law: ρ = P/(R_dT), where P is pressure, R_d is a constant, and T is temperature. To account for this dependency, let us substitute this expression into (6).

∂P = – (P/(R_dT)g∂z           (7)

For the math nerds, (7) is a separable first order partial differential equation if we make the assumption that T is an average temperature for the entire atmosphere. Ignoring the fact that this is a partial differential equation and, instead, treating it as if it was an ordinary differential equation, one gets the following result.

P = P₀e^{– z/H}                           (8)

P is pressure at altitude z. P₀ is the pressure at sea level.  H is a collective constant called the scaling factor. (On average, H is approximately equal to 7.5km.)

Let us now confirm that this equation is approximately correct by returning to our notes from the graph.

1. Notice that, if altitude increases in the equation, pressure decreases exponentially, not linearly. Thus, as pressure decreases, altitude increases exponentially. That part checks out well.
2. If about eighty percent of atmospheric pressure is below Mt. Everest, then twenty percent must reside above it. Thus, P/P₀ = 0.20. If we solve for z in (8) using this information, we find that the altitude of Mt. Everest is roughly 12km, which is pretty close to the illustration’s scale.

Thus, we can conclude with some confidence that the average pressure structure of the atmosphere in the vertical direction can be modeled by an exponential decay function as a consequence of hydrostatic balance.

Two weeks ago, Hannah asked an excellent question: Will meteorology ever be an exact science? The quick and dirty answer is no, absolutely not. To illustrate why this is so, however, I am going to use a specific example usually taught in an introductory atmospheric science course. Before doing so, I am going to make a few definitions clear so that everyone is on the same page.

The atmosphere is a fairly complex system in its entirety, so we generally divide it into different layers, each of which has its own special attributes. The layer closest to the surface of the Earth is called the troposphere. In general, it extends ten to sixteen kilometers above the Earth, varying depending where you are at the surface. About eighty percent of the atmosphere’s mass is contained within the troposphere, making it (understandably) the layer of air most responsible for our weather.

The shallow layer of the troposphere closest to the Earth (the layer in which we reside) is often referred to as the atmospheric boundary layer. It typically extends no more than a kilometer above the surface of the Earth. If the troposphere is responsible for weather, then, by analogy, the boundary layer is responsible for mixing air in just the right proportions to make that weather possible. This makes studying the boundary layer extremely important to meteorology, more specifically forecasting.

Often times when atmospheric scientists study the boundary layer, they wish to see how thermal energy is being transported. Is heat traveling upwards in the boundary layer, making clouds and other phenomenon possible, or is heat traveling downwards, having the opposite effect? To quantify this transportation of thermal energy in the boundary layer, we calculate sensible heat fluxes. In a nutshell, sensible heat fluxes look at the amount of thermal energy passing through some area over a given time. If the sensible heat fluxes are positive, then we can deduce that thermal energy is moving upwards in the boundary layer. Conversely, if the sensible heat fluxes are negative, then thermal energy is moving downwards. Sensible enough, right?

Mathematically speaking, sensible heat flux Q_H is given by the following formula: Q_H = ρc_p(θ’w’)_avg. While there are other components in this equation, I want to focus our attention on the last quantity: (θ’w’)_avg. This expression is what is known as a Reynolds average. In effect, it tries to take into account all of the slight up/down movements of thermal energy in the boundary layer to get a sense as to whether or not there is a significant net movement upwards or downwards of that thermal energy.

This, I hope you realize, is almost impossible to do. We would need a lot of data to notice all of the slight nuances of thermal energy movement in the boundary layer. Worse yet, if we did have enough data, these perturbations in thermal energy would change rapidly over time; the simplest actions…such as a butterfly flapping its wings…can disrupt energy balance in the boundary layer.

The inability to quantify or predict all variables influencing the boundary layer is a large outcome of what is known as The Butterfly Effect. Because we lack sufficient data and because the state of energy balance in the boundary layer is so chaotic, forecasting meteorologists find it impossible to predict weather phenomenon more than a few days out. While we may be able to add a few more days to the weekly planner in the future, there will come a time when we cannot forecast any further out, and it all comes down to that Reynolds average and its dependency on The Butterfly Effect.

As always, if you have more meteorology questions, feel free to post them in the comment section below.

Welcome back to a new semester, everyone! I hope you enjoyed my previous passion blog Musings of a Math Nerd. (If you have not yet seen the exciting conclusion to the series, I urge you to go back and look over the material.) Here, I embark upon a new journey–one less theoretical than the first, but equally exciting! Together, we will discover the world of weather around us, asking ourselves the basic questions that make our atmosphere so unique.

Unlike my previous series, these forthcoming blogs will be sustained by your own inquiries. Feel free to drop any sort of question pertaining to meteorology in the comment section below, and I will see to it that the question is answered in the subsequent blog. Have a great spring semester!

–Ryan

———

The air around us is filled with millions of microscopic pollutants.  Water vapor molecules in the air are continuously attaching and detaching themselves from these pollutants, forming a thin surface of liquid water around them. Meteorologists commonly refer to these droplets as haze. It is important to note that haze is not a cloud; rather, it is an obstruction to visibility. To become a cloud, haze particles must be enlarged. How to do this requires a pretty sophisticated idea called Kholer Theory.

At first the idea seems simple: To enlarge the haze particles requires the addition of more water vapor molecules from the surroundings into the liquid water surface. However, upon further inspection, there are two conditions that must be satisfied before one can make such a statement. The first condition considers the curvature of the droplet, called the Kelvin Effect. The second condition considers the purity of the liquid water, called Raoult’s Law.

What makes liquid water liquid? (Alternatively, what holds water molecules together?) The answer is the electrostatic attraction among electrons of one water molecule and protons of a different water molecule. Formally, in the case of water, we call this attraction a hydrogen bond. Notice that, if a surface of water is completely horizontal, a water molecule on the surface has many chances to make hydrogen bonds with its neighbors. What if the water was shaped into a sphere? If the water was shaped into a sphere, a water molecule on the surface would have noticeably smaller chances to make hydrogen bonds because it does not have as many neighbors as in the flat-surface case. Because a smaller number of bonds are holding the water molecule in the liquid state, it is more likely to escape as a vapor molecule.

Thus, the Kelvin Effect tells us that droplets are more likely to give away their water molecules, not accept more.

Sketch a sample of pure water molecules in liquid phase. Sketch a sample of water molecules in liquid phase with solutes in it. Would you not agree that the solutes are occupying sites where water molecules could likely escape from the sample? Because solutes are occupying this space, it might be fairly accurate to say that impure liquid water, i.e. water with substances dissolved within it, does not as easily give up its water molecules. This conclusion is, in fact, called Raoult’s Law.

Thus, Raoult’s Law tell us that droplets in the atmosphere, which are likely not comprised of pure liquid water, are likely to keep their water  molecules, not give them away.

It appears we have reached two contradictory conditions. Haze droplets can be self-limiting because of their curvature but also have the property to store what little they have fairly well because of their impurities. Kohler Theory combines these two effects to give us a better way to understand how haze droplets actually behave.

The above is a sketch of what is called a Kohler Curve. It represents graphically what happens when the Kelvin Effect and Raoult’s Law are combined. The x-axis represents the radius of the drop. The y-axis is a measure of the amount of water vapor molecules needed from the surrounding air.

Notice that the Kohler Curve has a maximum value at (r_c,S_c). If we add S_c of water vapor molecules from the surrounding air (or more), our haze droplet will grow to a radius of r_c and then continue to grow, forming a cloud drop.

Thus, Kohler Theory tells us that, for some determined lower-bound number of water vapor molecules from the surroundings, a haze drop will grow into a cloud drop. If the lower-bound number of water vapor molecules from the surroundings is not satisfied, a haze drop will not become a cloud drop.

———