Bilayer graphene exhibits ground states that can be polarized in spin, valley, or orbital. These ground states can be controlled with applied magnetic and electric fields or by reducing the distance between layers with uniaxial pressure.

We study the ground state phase diagram treating the Coulomb interaction between electrons at the Hartree-Fock level. We show that pressure and magnetic field are direct experimental methods for tuning the balance between the Landau level separation (noninteracting energy scale) and the exchange energy (interacting energy scale). We predict that using pressure to tune this balance, five ordered states can be observed, two of which are only accessible with applied pressure. These states are both orbitally polarized. One is maximally orbitally polarized but unpolarized in valley and spin, while the other is partially polarized in orbital and spin but unpolarized in valley.

We posted this paper posted in the arxiv, and has been published in Physical Review B.

See also the video presentation of Brett Green at the March Meeting 2020.

Key results:

Below are the phase diagrams depicting the five possible ground states in our model and magnetic field, electric field, and pressure which may be used to construct them. The legend at the bottom indicates which Landau levels are filled and hence in which degrees of freedom the state is ordered.

Abstract:

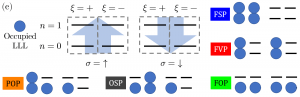
Bilayer graphene in a magnetic field hosts a variety of ordered phases built from eight Landau levels close in energy to the neutrality point. These levels are characterized by orbital n=0,1, valley ξ=+,- and spin σ=↑,↓; their relative energies depend strongly on the Coulomb interaction, magnetic field, and interlayer bias. We treat interactions at the Hartree-Fock level, including the effects of metallic gates, layer separation, spatial extent of the p_z; orbitals, all Slonczewski-Weiss-McClure tight-binding parameters, and pressure. We obtain the ground state as function of the applied magnetic field, bias, and pressure. The gates, layer separation and extent of the p_z orbitals weaken the Coulomb interaction at different length scales; these effects distort the phase diagram but do not change its topology. However, previously-predicted continuous transitions become discontinuous when all tight-binding parameters are included nonperturbatively. We find that pressure increases the importance of the noninteracting scale with respect to the Coulomb energy, which drives phase transitions to occur at lower fields. This brings two orbitally polarized states not yet predicted or observed into the experimentally accessible region of the phase diagram, in addition to previously-identified valley-, spin-, and partially orbitally polarized states.