On the Dynamics of Some Complex Fluids [PDF]
Francesco De Anna (Penn State University)
In this talk we analyze the dynamics of nematic liquid crystals, through the models proposed by:
– Ericksen and Leslie,
– Beris and Edwards,
– Qian and Sheng.
We establish some well-posedness results, such as existence and uniqueness of global-in-time weak or classical solutions. The general framework for the initial data is that of Besov spaces. Some regularizing effects for the heat kernel, as the so-called “Maximal Regularity Theorem”, play a main role in the proof, as well as the Littlewood-Paley theory and the paradifferential-calculus.
Special Properties of the Electric Field [PDF]
Bob Eisenberg (Rush University)
In mathspeak:
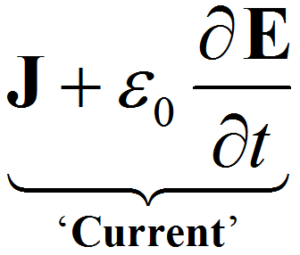 is conserved exactly, always, everywhere.
is conserved exactly, always, everywhere.
In words,
Charges are everywhere because most atoms are charged. Chemical bonds are formed by electrons with their charge. Charges move and interact according to Maxwell’s equations in space and in atoms where the equations of electrodynamics are embedded in Schrödinger’s equation as the potential. Maxwell’s equations are universal, valid inside atoms and between stars from times much shorter than those of atomic motion (0.1 femtoseconds) to years (32 mega-seconds).
Maxwell’s equations enforce the conservation of current. Analysis shows that the electric field can take on whatever value is needed to ensure conservation of current.
The properties of matter rearrange themselves to satisfy Maxwell’s equations and conservation of current. Conservation of current is as universal as Maxwell’s equations themselves.
Equations of electrodynamics find little place in the literature of material physics, chemistry, or biochemistry. Kinetic models of chemistry and Markov treatments of atomic motion are ordinary differential equations in time and do not satisfy conservation of current unless modified significantly. Systems at equilibrium, without macroscopic flow, have thermal fluctuating currents that are conserved according to the Maxwell equations although their macroscopic averages are zero. The macroscopic consequences of atomic scale fluctuating thermal currents are not known but are likely to be substantial because of the nonlinear interactions in systems like these, in which ‘everything interacts with everything else’.
The material in this lecture is presented in detail in arXiv ref 1607.06692016. I recommend having a copy in sight (in hand or in computer).
An extended discussion is found in arXiv ref 1502.0725, which has been published as Mass Action and Conservation of Current, Hungarian Journal of Industry and Chemistry (2016), 44: 1-28. The extended discussion beginning on p.6 of Fig. 2 is likely to be useful.
Energetic Variational Approach to Multi-Component Fluid Flows [PDF]
Arkadz Kirshtein (Penn State University)
In this talk I will introduce the systematic energetic variational approach for dissipative systems applied to multi-component fluid flows. These variational approaches are motivated by the seminal works of Rayleigh and Onsager. The advantage of this approach is that we have to postulate only energy law and some kinematic relations based on fundamental physical principles. The method gives a clear, quick and consistent way to derive the PDE system. First I will show the derivation of two-component phase-field model. Then I will highlight different approaches to three-component flows. If time permits, I will discuss the importance of boundary effects and its impact on the dynamics.
Poisson-Boltzmann type models for electric double layers [PDF]
Tai-Chia Lin (National Taiwan University)
In this lecture, two kinds of PB (Poisson-Boltzmann) type models will be introduced for the study of electric double layers, which include the Debye and Stern layers. One is the CCPB (charge conserved Poisson-Boltzmann) equation and the other is the PB_{ns} equation (new Poisson-Boltzmann equation with steric effects). Using analytical techniques to study the CCPB equation, we may derive an explicit formula for the mixture of Na^{+}, Mg^{2+} and Cl^{-} which can be justified by experiments using atomic force microscopy. Besides, radial solutions of CCPB equations with variable coefficients are investigated. Under specific parameter regimes, the PB_{ns} equation (which is obtained by a new approach to the Lennard-Jones potential) may be reduced to the PB type models of D. Andelman (1997) and B. Li (2009). It would be expected that the PB_{ns} equation may have more applications on electrolytes with high concentrations of ions.
Interfacial deformation due to an impinging disk between two fluids: experimental results
Zahra Niroobakhsh (Penn State University)
TBA
Calculating Energy Barriers and Activation States for Steps of Fusion
Rolf J. Ryham (Fordham University)
Fusion between biological membranes is a widespread cellular process, responsible for events as varied as secretion of neurotransmitters and fertilization of egg by sperm. Molecularly, fusion is the merger of two lipid bilayer membranes,and this merger proceeds through several key intermediates states. But the transition energy barriers that separate these intermediates have not been determined. Using the string method, we calculate a least energy pathway and the activation states between intermediates for the entire fusion process. The bilayer energetics are based on a modified Helfrich Hamiltonian that accounts for long range interactions between bilayers, and a novel field theoretic treatment of hydrophobic potentials. Through the energetic analysis, we conclude that lipid demixing is required for the transition from a stalk to a hemifusion diaphragm, and that complete fusion is possible provided pore formation is initiated while the diaphragm is small. The calculations provide a movie of individual lipid deformations, as the membrane geometry and topology evolve over time.
On an Optimal Boundary Control Problem for Incompressible Nematic Liquid Crystal Flows in 2D [PDF]
Hao Wu (Fudan University)
In this talk, we will present the optimal boundary control problem for a simplified Ericksen-Leslie system modelling the incompressible nematic liquid crystal flows in two dimensions. We suppose that the fluid velocity satisfies a no-slip boundary condition, while the equation for the molecular orientation is subject to a time-dependent Dirichlet boundary condition. The existence of optimal boundary controls and first-order necessary conditions of optimality will be discussed.
