Introduction
Platinum is a chemical element with symbol Pt and atmomic number 78. The electron configuration is [Xe] 4f145d96s1. Its crystal structure is face-centered cubic (fcc, see Fig. 1 ), and the lattice constant is 3.9239 Å[1].
), and the lattice constant is 3.9239 Å[1].
The target for this computation experiment is to use density functional theory (DFT) to evaluate the energy of fcc lattice at different lattice constants. The estimation of the lattice constant is hence decided by minimizing the energy. The result is compared with the standard data based on experimental measurements.
Key Factors of Density Functional Theory (DFT)
Denstity functional theory (DFT) is a computational method based on calculating the energy of a condensed matter system as a functional of the electron density. Thereare a lot of references that give systematic introductions and discussions on the method, which we will not go into details in this report[2]. The key factors affecting the calculation in this report include (1) Energy cut-off and (2) k-point sampling number. Energy cut-off refers the maximum energy of the bands involved in our calculation. The number of the bands included for a typical calculation is about 20, and this number may increase when higher energy resolution is required. K-point sampling number refers the number of sampling points within the first Brillouin zone. Usually the higher the energy cut-off is and the larger the sampling number is, the better the accuracy is. Due to limitation on the computational resources, we have to decide lowest values of both the factors that could meet requirements.
We performed several trial calculations and compared their numerical variance to decide the appropriate values. (1) We fix the cut-off energy at 800 eV, which is high enough for a simple calculation, and explore the effect of k-point density on energy calculation and atomic energy to figure out the minimum sufficient value for k-point sampling number. (2) We use the number of k-point sampling mentioned above and explore the effect of cut-off energy and decide the best cut-off energy that balances the calculating speed and precision. Both tests are performed at conventional lattice constant a=4Å.
Energy Evaluation and Lattice
Applying the parameters decided above, several calculations of free energy at lattice constant ranging from 3.4 ~ 4.4Å were performed. Then a quadratic fitting was performed to minimizing energy. The corresponding lattice constant is our theoretical prediction of the true lattice, and it is compared with standard value. A more detailed discussion can be found in the experimental section in this report.
Experimental Facts
The basic parameters and key factors shared in all the calculations are listed below:
Lattice cell type: primitive cell of face centered cubic (fcc)
Functional Type: GGA PBE
Smearing width: 0.10
Pseudo Potential Orbitals: 4f14 5s2 5p6 5d9 6s1
Pseudo Type: OTFG ultrasoft
k-points origin shift: no
K-point Number Examination
Based on the discussion above, we calculated the free energy of the lattice at a=4Å. The results are shown in Fig. 2. Based on this result, it is sufficient to choose 16×16×16 as the appropriate sampling number for one wants acceptable precision without spending too much time.
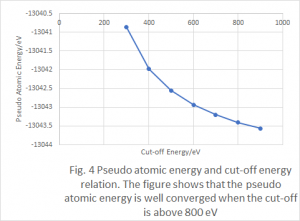
Energy Cut-off Examination
The convergence of energy and pseudo atomic energy are displayed as follows. The difference between them is the binding energy per atom. Although it is not fully converged, the pseudo atomic energy variance is highly suppressed when the cut-off energy is higher than 800eV, which indicates that 800eV is a reasonable choice for our estimation of the binding energy (Fig.3 and Fig.4).
Energy at Different Lattice Constants
To best fit the plots in the graph, a polynomial to the order of 3 was applied, and the minimum free energy was reached at lattice constant a=3.95Å. Compared to the standard result, this calculation has an error of 0.6%.
Reference
[1] https://en.wikipedia.org/wiki/Platinum
[2]Sholl, David, and Janice A. Steckel. Density functional theory: a practical introduction. John Wiley & Sons, 2011.