Overview of the Problem
This post will be about determining both the structure and lattice constant for platinum. This will be done using density functional theory (DFT) to calculate the cohesive energies across a range of lattice parameters for platinum in the simple cubic (SC), face-centered cubic (FCC), and hexagonal close-packed (HCP) structures.
In order to make sure the results are feasible, convergence tests are first done for both the number of k-points and the cutoff energies.
All calculations are done in Materials Studio with the CASTEP DFT package [1]. The functional used was that of Perdew Burke Ernzerhof [2], and the pseudopotential was obtained using the Koelling-Harmon solver for the 4f14 5s2 5p6 5d9 6s1 outer shells.
Cutoff Energy Convergence
The cutoff energy was tested by starting at a cutoff energy of 360 eV and then increasing by increments of 30 eV to look for convergence in the free energy. For this test the lattice parameters of the three structures were chosen as a = 3.92 Å for FCC, a = 2.62 Å for SC, and a = 3.02 Å, c = 4.83 Å for HCP. These lattice constants were chosen for this test by roughly estimating the location of the minimum of the three structures at an energy cutoff of 300 eV. The results are outlined in table 1 and figure 1.
| Energy Cutoff (eV) | FCC Free Energy (eV) | SC Free Energy (eV) | HCP Free Energy (eV) |
|---|---|---|---|
| 300 | -13050.818 | -13050.421 | -13049.923 |
| 330 | -13050.927 | -13050.534 | -13050.046 |
| 360 | -13050.960 | -13050.568 | -13050.080 |
| 390 | -13050.970 | -13050.578 | -13050.116 |
| 420 | -13050.973 | -13050.580 | -13050.119 |
| 450 | -13050.973 | -13050.581 | -13050.120 |
| 480 | -13050.974 | -13050.581 | -13050.120 |
| 510 | -13050.974 | -13050.581 | -13050.120 |
As can be seen from the figure and the table, a lower energy cutoff here will overestimate the free energy. It can also be see that the variation in the free energy is less than 0.01 eV past the 390 eV cutoff energy. For consistency, a cutoff energy of 420 eV has been chosen for all calculations involving the determination of the lattice parameters.
K-Point Convergence
The k-point convergence was tested using an HCP structure with a = 3.12 Å and c/a = 1.6, an SC structure with a = 2.62 Å, and an FCC structure with a = 3.92 Å. The results are outlined in tables 2, 3, and 4, as well as figures 2, 3, and 4.
| K-point Grid | Number of K-points | Free Energy (eV) |
|---|---|---|
| 7x7x4 | 32 | -13050.000 |
| 8x8x5 | 156 | -13049.970 |
| 9x9x6 | 75 | -13049.970 |
| 10x10x6 | 240 | -13049.965 |
| 11x11x7 | 144 | -13049.955 |
| 12x12x8 | 456 | -13049.975 |
| 13x13x9 | 196 | -13049.970 |
| K-point Grid | Number of K-points | Free Energy (eV) |
|---|---|---|
| 6x6x6 | 28 | -13050.960 |
| 8x8x8 | 20 | -13050.94 |
| 10x1010 | 110 | -13050.943 |
| 11x11x11 | 56 | -13050.945 |
| 12x12x12 | 182 | -13050.945 |
| 13x13x13 | 84 | -13050.943 |
| 14x14x14 | 280 | -13050.943 |
| 15x15x15 | 120 | -13050.945 |
| 16x16x16 | 408 | -13050.945 |
| K-point Grid | Number of K-points | Free Energy (eV) |
|---|---|---|
| 10x10x10 | 35 | -13050.460 |
| 11x11x11 | 56 | -13050.470 |
| 12x12x12 | 56 | -13050.490 |
| 13x13x13 | 84 | -13050.500 |
| 14x14x14 | 84 | -13050.510 |
| 15x15x15 | 120 | -13050.500 |
| 16x16x16 | 120 | -13050.500 |
Figure 2: K-point convergence plot for SC
Figure 3: K-point convergence plot for HCP
Figure 4: K-point convergence plot for FCC
For the SC lattice, having few k-points gives energies that start above the convergence level with a tendency to decrease. This is not the case for the HCP lattice, where the energies start low and then increase before decreasing again. Lastly, for the FCC lattice we see that the energy starts above the convergence level before sharply decreasing and then approaching convergence.
Based on the results from the test of the k-point convergence, grids of 15x15x15 were chosen FCC and SC, while a grid of 13x13x9 was chosen for HCP.
Lattice Parameter for SC
The simple cubic structure is shown in figure 5.
Figure 5: Simple cubic lattice structure
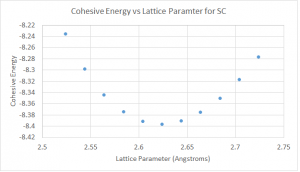
The calculations for the cohesive energy were done by first calculating the free energy per atom for the simple cubic structure, and then subtracting away the atomic energy of -13042.12 eV, which was obtained from the pseudopotential calculations. The results are shown in figure 6.
Figure 6: Cohesive energy vs lattice parameter for the simple cubic structure.
Pt in the simple cubic configuration is found to be stable with a lattice constant of a = 2.62 Å and a cohesive energy of -8.396 eV.
Lattice Parameter for FCC
The face-centered cubic structure is shown in figure 7.
Figure 7: The face-centered cubic lattice structure
The calculations of the cohesive energy were done in the same way as they were for the simple cubic lattice. The atomic energy will remain the same, so we simply calculate the free energy and take the difference. The results of these calculations are shown in figure 8.
Figure 8: Results from the calculation of cohesive energy for Pt in the FCC configuration for various lattice parameters
From the results of the calculation, it is found that Pt in the FCC configuration has a preferred lattice constant of about 3.96 Å, which gives a cohesive energy of -8.851 eV.
Lattice Parameter for HCP
The lattice of the hexagonal close-packed structure is shown in figure 9.
Figure 9: The hexagonal close-packed lattice structure
The HCP lattice has two lattice constants, so there is a much larger phase space to explore in order to locate the minimum cohesive energy. In order to sample this space, the ratio between the lattice constants, c/a, is held fixed at values of 1.57, 1.6, and 1.63. The parameters a and c are then varied in tandem to search for the preferred lattice constant. The results of these calculations are shown in figure 10.
Calculations for the cohesive energy of HCP Pt for c/a ratios of 1.57, 1.6, 1.63.
The results show that an HCP lattice of Pt is most stable with lattice constants of a = 2.98 Å and c = 4.77 Å for c/a = 1.6. These parameters give a cohesive energy of -7.996 eV.
Conclusions
The calculations done above give cohesive energies of -8.396 eV for SC, -8.851 eV for FCC, and -7.996 for HCP. This implies that Pt is most stable in the FCC configuration with a lattice constant of 3.96 Å. Davey finds through experimental methods that Pt is most stable in the FCC configuration with a lattice constant of 3.91Å [3]. Using density functional theory, we have shown that we can correctly predicted that Pt naturally forms an FCC lattice. However, we have overestimated the lattice constant by about 0.05 Å.
References
[1] First principle methods using CASTEP Zeitschrift fuer Kristallographie 220(5-6) pp. 567-570 (2005).
[2] Perdew, J.P., K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple.Physical review letters, 1996. 77(18): p. 3865.
[3] Davey, W. P. (1925). Precision Measurements of the Lattice Constants of Twelve Common Metals. Physical Review, 25(6), 753-761. doi:10.1103/physrev.25.753.
