Lingjie Zhou
Abstract
In this post, optimal lattice parameters of gold(Au) are analytically derived using Density Functional Theory(DFT) methods. Plane-wave basis set, pseudopotential DFT methods are used to calculate the energy dependence in Simple Cubic(SC), Face Centered Cubic(FCC) and Hexagonal Closest Packed(HCP) lattice system. The convergence of cutoff energy and the number of k points is also checked in this post.
Introduction
As well known, Au has a preferred lattice structure under Standard Temperature and Pressure(STD), which is FCC lattice with a=4.08Å. Single crystal gold is a good conductor and material for research purposes. Its good electronic properties make it one of the best platforms to conduct STM research. To predict which lattice structure is preferred, we need to compare the energy in different lattice structures. DFT can calculate the energy of the structures that don’t exist in nature, thus making it a powerful method to determine the optimal lattice structure theoretically. This can also enable us to predict the properties of materials that may not be normally present in experiments.
Methods:
The CASTEP[2] package is used to carry out the DFT calculation. The exchange-correlation functional is GGA-PBE. The ‘on the fly’ generated ultrasoft pseudopotential for Au has a core radius of 2.4 Bohr(1.27 Angstroms) and was generated with 32 electrons in the valence panel with (4f14 5s2 5p6 5d10 6s1) as the electronic configuration.
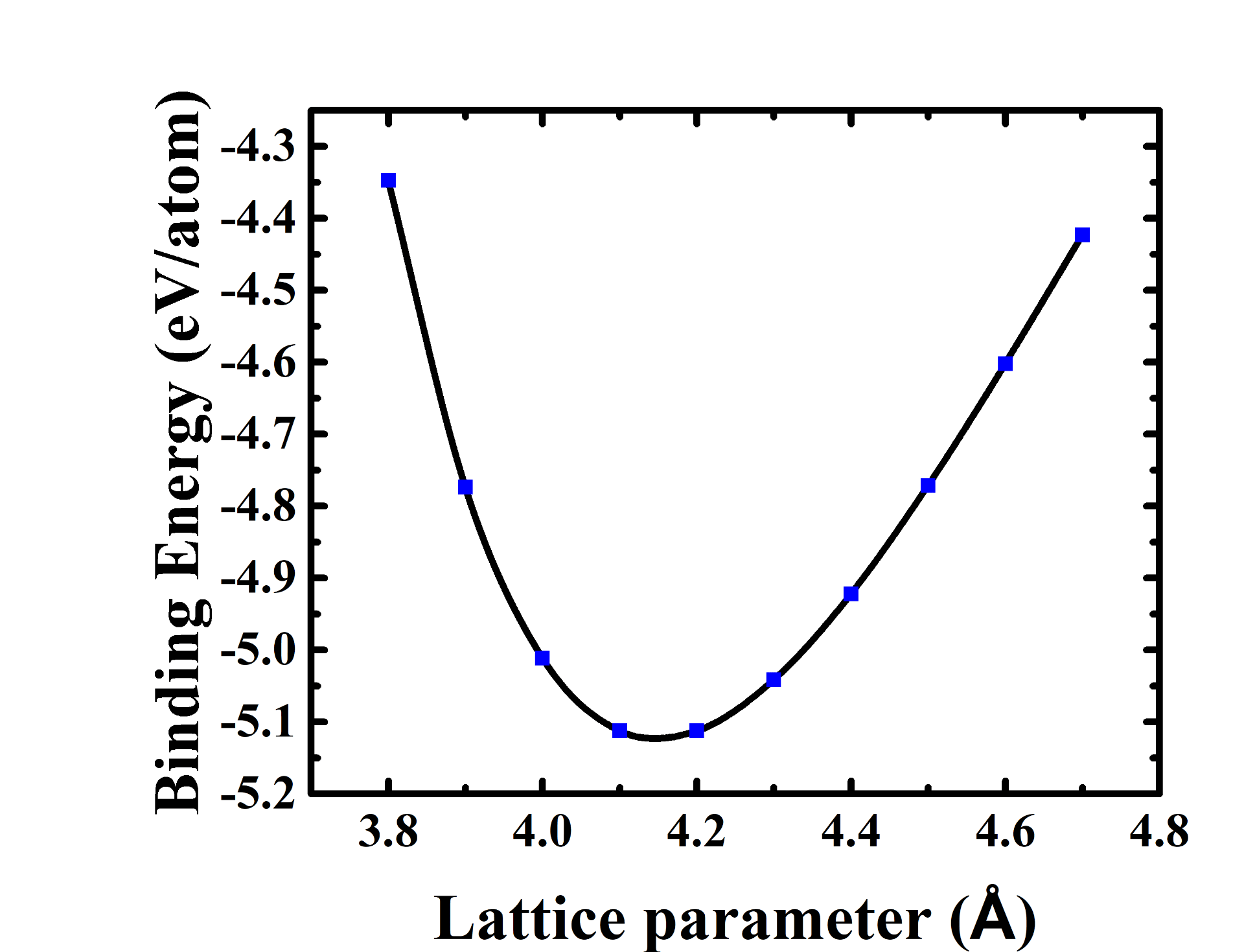
A kpoint set of 5×5×5 and cutoff energy 700eV is used to calculate the energy of SC and FCC lattice at different lattice parameters, while 10×10×5 kpoint mesh and 700eV cutoff energy is used for HCP lattice. The number of kpoint and cutoff is initially hypothesized as sufficient before checking convergence and the convergence will be further checked.
Figure 1 Lattice parameter optimization.a)SC using 5×5×5 kpoints and 700 eV cutoff energy 5b)FCC using 5×5×5 kpoints and 700 eV cutoff energy c)HCP using 10×10×5 kpoints and 700 eV cutoff energy
The SC lattice has its minimum energy at a=2.75Å, with E=-4.656eV. FCC lattice has its minimum energy at a=4.14 Å, with E= -5.12eV. For HCP lattice, there are two variables a and c. For fixed a/c ratio[1], the DFT can give the optimal a for the minimum energy. By comparing the minimum energy corresponding to different a/c ratio, HCP lattice has its minimum energy at a=2.91Å, a/c=1.68, with energy E=-5.018eV. Thus, the optimal lattice with these cutoff energy and kpoint choices is FCC lattice with a=4.14Å.
Cutoff energy test
The convergence of cutoff energy is tested using kpoint 5×5×5(a=2.75Å for SC and a=4.14 Å for FCC), 10×10×5(a=2.91Å, a/c=1.68 for HCP).
Figure 2 Convergence test for the cutoff energy. a) SC with 5×5×5 kpoints, a=2.75Å b)FCC with 5×5×5 kpoints, a=414Å c) HCp with 10×10×5 kpoints, a=2.91Å, a/c=1.68
The total energy does not change more than 0.01eV beyond 400eV(SC), 500eV(FCC) and 400eV(HCP). So that the cutoff energy we used(700eV) is well satisfied.
Kpoint convergence test
After checking the convergence of cutoff energy, we need to make sure our calculation is also convergent under number of k points. Here we will check the kpoint convergence at the optimal values for the different lattices.
Figure 3 Convergence test for the kpoints. a) SC with a=2.75Å b)FCC with a=4.14Å c) HCp with a=2.91Å, a/c=1.68. All with cutoff eneryg 700eV
The cutoff energy is 700eV for the kpoint convergence test. The energy is converged in the range of 0.01eV beyond 35 kpoints(9×9×9) for SC, 110 kpoints(10×10×10) for FCC and 120(16×16×8). The well converged total energy is -4.8149 for SC (a=2.75Å, 9×9×9, 700eV), -5.0174eV for FCC(a=414Å, 10×10×10, 700eV) and -5.011eV for HCP(a=2.91Å, a/c=1.68, 16×16×8, 700eV).
Conclusion:
| Lattice Structrue | Mesh of k point | Cutoff energy | optimal lattice parameters(Å) | Binding Energy(eV) |
|---|---|---|---|---|
| SC | 9×9×9 | 700 | a=2.75Å | -4.8149 |
| FCC | 10×10×10 | 700 | a=4.14 Å | -5.0174 |
| HCP | 16×16×8 | 700 | a=2.91Å a/c=1.68 | -5.011 |
The lowest energy phase of Au crystal was calculated to be FCC lattice structure with a=4.14Å. The experimental result is 4.08Å in FCC lattice structure[3], which is slightly smaller than the lattice parameters calculated.
Reference: