Author: Andrew Wong

1. Introduction

Palladium is a transition metal that is vital in various technologies, such as in electronic components and fuel cells, and as an important catalytic material [1]. The goal of this post is to determine the preferred crystal structure of Palladium (Pd) based on the following three crystal structures: simple cubic (SC), face-centered cubic (FCC), and hexagonal closed packed (HCP). In order to determine the optimal crystal structure of Pd, plane wave basis Density Functional Theory (DFT) was implemented with the CAmbridge Series Total Energy Package (CASTEP) [2] in Materials Studios to calculate ground state energies of various crystal structures of Pd at different lattice constants. The lowest total energy of the three crystal structures are then compared to determine the optimal crystal structure of Pd and its respective lattice constant.  From these calculations, the optimal lattice constants of the SC and FCC structure were determined to be 2.6 Åand 3.85 Å. Since the HCP crystal structure has two lattice parameters, the optimal lattice constant of HCP were a=2.9 Å and c= 5.04 Å from an optimal c/a value of 1.8. Comparing the energy per atom of each crystal structure, the FCC structure had the lowest structure while the SC and HCP structure were 0.217 and 0.514 eV/atom higher in energy than the FCC structure. As a result, the optimal crystal structure for Pd is the FCC structure with a lattice constant of 3.85 Å.

2. Methodology

2.1 Calculation Parameters

The DFT calculations performed in this post utilized the plane wave basis set with pseudo potentials method in CASTEP. The following calculation parameters used in the DFT analysis are shown below..

2.2 Energy Cutoff Determination

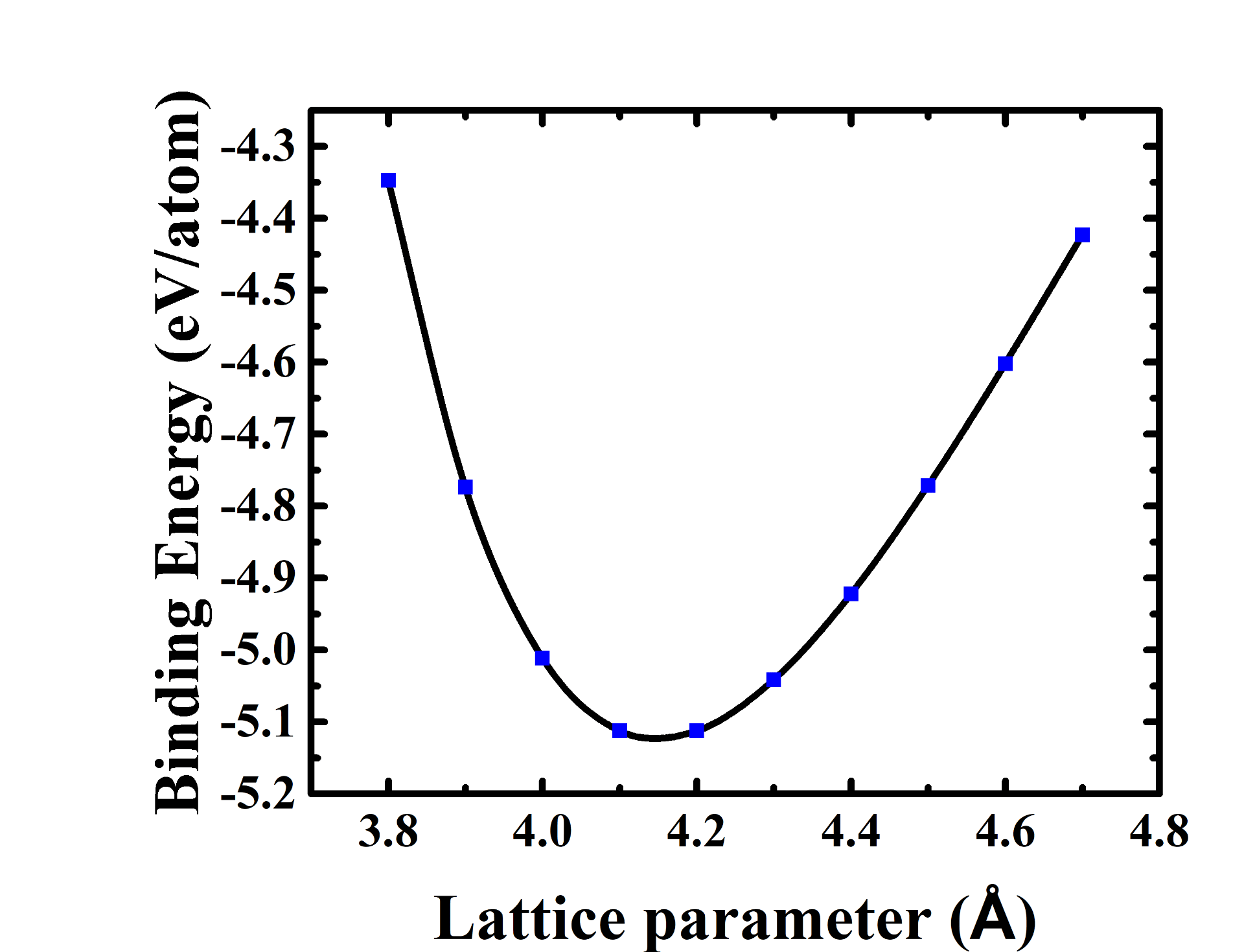
Before the optimal lattice constant and K Points for each structure were determined, an energy cutoff optimization was performed to ensure the most accurate convergence of the energy calculations. The optimal energy cutoff value is then used for all three crystal structure to maintain consistency within the calculations. A FCC Pd crystal structure with an experimental lattice constant of 3.859 Å [4] and default K Point mesh grid of 7 x 7 x 7 was used to test for energy cutoff convergence. By varying the energy cutoff values from 100 to 600 eV, a plot of total lattice energy per atom and energy cutoff is shown below in figure 1.

Figure 1: Energy Cutoff Convergence for FCC Pd

Based on the results from figure 1, the energy cutoff for all DFT optimization calculations was chosen to be 500 eV since the energy per atom varied less than 0.01 eV at the cutoff energy. A higher energy cutoff value, such as 600 eV or more, could have been chosen as it retains but the computational effort to run these calculations would increase. As a result, a cutoff energy of 500 eV was deemed to be optimal for the lattice calculations.

2.3 K Point Optimization

A convergence test for K Points was implemented to further ensure the energy convergence of the three crystal structures. A K Points Optimization for each crystal structure must be implemented as the number of K Points directly dependent on the lattice constant value. Lattice constants for each structure were determined using the default 7 x 7 x 7 K Point Mesh Grid  for the SC and FCC crystal structure and a 8 x 8 x 4 K Point Mesh Grid for the HCP crystal structure. The lattice constants that were determined from the default K Point mesh for the SC, FCC, and HCP structure were respectively 2.3 Å, 3.8 Å, a= 3Å and c= 5Å.

2.3.1 K Points Optimization for SC and FCC Structure

A convergence test for K Points was implemented to further ensure the energy convergence of both the SC and FCC crystal structures. This was conducted by plotting the total energy per atom of each structure with respect the number of irreducible K Points. Since the lattice constant, a, is constant on all three axis for the SC and FCC crystal structure, a Monkhorst-Pack Grid of M x M x M is utilized for K Points optimization. For both structures, an energy cutoff value of 500 eV was implemented. For the SC Structure, figure 2A was constructed below by varying the K Point Mesh size from 1x1x1 to 15x15x15 at the  SC lattice constant of 2.3 Å.

Figure 2A: K Point Determination for SC Pd Crystal Structure

As seen in figure 2A, the optimal number of K Points was determined to be 56 and a mesh grid size of 11 x 11 x 11. Higher number of K Points could have been implemented but the amount of computational effort would have increased significantly. As a result, the optimal number of K points for the simple cubic Pd structure was deemed to be 56. The energy at this number of K Points is -3492.550 eV.

Similarly, the optimal number of K Points needed for the Pd FCC crystal structure was shown below in figure 2B by varying the K Point mesh size from 1x1x1 to 10x10x10 at the optimal FCC lattice constant of 3.8 Å.

Figure 2B: K Point Determination for FCC Pd Crystal Structure

As seen in figure 2B, the optimal number of K Points was deemed to be 365 with a K Point mesh size of 9 x 9 x 9. The energy at this number of K Points is -3493.064 eV.

2.3.2 K Points Optimization for HCP Structure

Although the HCP K Point mesh grid is in the form of M x M x N, the same K Point convergence method used for the SC and FCC structure can be used for the HCP structure. By using a cutoff energy of 500 eV and lattice constant values of a = 3 Å and c = 5 Å, figure 2C was constructed below by plotting the total energy per atom with respect to the number of irreducible K points, varying the K Points mesh grid from 1x1x1 to 10x10x5.

Figure 2C: K Point Determination for HCP Pd Crystal Structure

From figure 2C, it was determined that the optimal number of K Points for the HCP Pd Crystal structure is 162 with a Mesh Grid of 9 x 9 x 4. The total energy per atom at this specific K Point value was -3492.847 eV.

3. Results and Discussion

3.1 Lattice Optimization of Simple Cubic and Face-Centered Cubic Pd

The optimal lattice constants for both the SC and FCC crystal structures were determined by calculating the total energy of the structure at various lattice constant values. Once this is completed, the optimal lattice constant corresponds to the structure with the lowest total energy. The SC lattice constants were varied from 2.2 to 3.4 Å and the FCC lattice constants were varied from 3 to 4.4 Å. Both the SC and FCC energies were then plotted against its respective lattice constant with a K Point mesh size of 11 x 11 x 11 and 9 x 9 x 9 respectively and an energy cutoff value of 500 eV. The lattice constant determination for the Pd SC structure is shown below in figure 3A.

Figure 3A.: Lattice Constant Determination for Simple Cubic Pd Crystal Structure

A polynomial fit was employed to determine the minimal energy of the Pd SC structure. As a result, the optimal lattice constant for the Pd SC structure was determined to be 2.6 Å at a total energy per atom value of -3492.711 eV. Following a similar process, the lattice constant was determined for the Pd FCC structure in figure 3B below.

Figure 3B: Lattice Constant Determination for FCC Pd Crystal Structure

By varying the lattice constant from 3 to 4.4 Å and employing a third order polynomial fit, the minimal structural energy was calculated at a value of -3493.131 eV, which resulted in an optimal FCC lattice constant of 3.85 Å.

3.2 Lattice Optimization of Hexagonal Closed-packed Pd

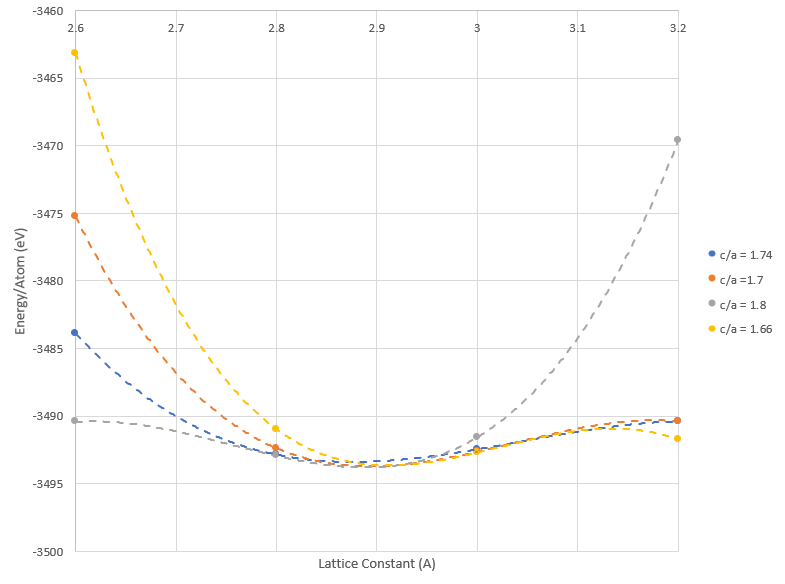
Unlike the SC and FCC structure, two lattice constants, a and c, must be determined for the HCP crystal structure. However, the DFT energy optimization used for the SC and FCC structure can still be implemented by fixing a lattice parameter ratio, c/a, and calculating the energy of the HCP structure at various lattice constant of a. Since there are two lattice constants values in the HCP structure, the K Point mesh grid is in the form of M x M x N. As a result, a K Point mesh grid size of 9 x 9 x 4 and a cutoff energy of 500 eV was implemented for the HCP DFT lattice optimization. By varying the c/a from 1.66 to 1.8 Å, Figure 3C  was constructed below by plotting the total energy per atom with respect to the optimal lattice constants, varying the “a” lattice constant from 2.6 to 3.2 Å.

Figure 3C: Optimal Lattice Constant Determination for HCP Pd Crystal Structure

Before the optimal lattice constant can be determined, polynomial fits for each c/a ratio was implemented to determine which lattice parameter ratio had the lowest energy minimum. As a result, the lowest energy minimum occurred at a c/a ratio of 1.8 at an energy of -3492.935 eV. Furthermore, the optimal HCP lattice constants for Pd was determined to be a = 2.9 Å and c = 5.04 Å.

4. Conclusion

The table below shows a summary of the optimal lattice constant, energy cutoff, and K Points calculated for each of the three crystal structures at its minimized total energy.

From the data above, it is concluded that the preferred structure for Pd is FCC with a lattice constant of 3.85 Å since this is the structure with the lowest total energy per atom. To confirm the validity of our result, the lattice constant and structure of Pd was then compared to an experimental paper as reference which is shown below.

As seen from the table above, the DFT calculations are in agreement with the experimental source in terms of the lattice constant and the preferred crystal structure. Differences between the lattice constants are expected as the DFT calculations assume the model contains perfect shapes of each Pd crystals and is run in vacuum. In conclusions, the following DFT energy optimization technique implemented in this post confirms the preferred crystal structure of Pd to be Face-centered cubic with a lattice constant of 3.85 Å.

5. Citations

[1] “Palladium.” Wikipedia, Wikimedia Foundation, 3 Feb. 2020, en.wikipedia.org/wiki/Palladium.

[2] Clark Stewart J et al., “First principles methods using CASTEP ,” Zeitschrift für Kristallographie – Crystalline Materials , vol. 220. p. 567, 2005.

[3] H. J. Monkhorst and J. D. Pack, “Special points for Brillouin-zone integrations,” Phys. Rev. B, vol. 13, no. 12, pp. 5188–5192, Jun. 1976.]

[4] Davey, Wheeler P. “Precision Measurements of the Lattice Constants of Twelve Common Metals.” Physical Review Journals Archive, American Physical Society, 1 June 1925,

Introduction

Zirconium single crystal is experimentally observed to have two different crystal structures. The high-temperature β phase zirconium is a bcc structure while the room temperature α phase zirconium is in hcp structure [1]. The experimentally observed lattice constant for hcp structure α-zirconium by Goldak et al. is a= 3.22945 Å and c= 5.14139 Å at 4.2 K [2]. The room temperature lattice parameter reported by Easton and Betterton is a= 3.2327 Å and c= 5.1471 Å [3].

Density functional theory (DFT) calculation with generalized gradient approximation (GGA) is regarded to be a powerful tool for determining properties of bulk single crystals [4,5]. In this work, we used DFT calculation to predict the lattice constant for α-zirconium. We first fix a/c ratio and calculate energy corresponding to different lattice constants. The lattice parameter corresponding to the lowest energy is the predicted lattice parameter. Our calculated result is then compared to the experimentally observed one to verify the accuracy of density functional theory in calculating lattice parameters for single crystals.

Computational details

Crystal Structure

The unit cell of Zr single crystal was built according to data from Materials Project. The space group of α-zirconium is P6₃/mmc (194). The lattice constant ratio (c/a) is set to 1.592 and the γ angle was set to be 120 degrees. There are two atoms in the unit cell of α-zirconium and the coordinates are (0.3333,0.6667,0.25) and (0.6667,0.3333,0.75). The built α-zirconium is shown in Figure 1.

Figure 1 α-zirconium in hcp structure. The blue atoms are zirconium atoms and the red line indicates the unit cell of α-zirconium.

Convergence test

Our calculation used plane-wave bases with on the fly generated ultrasoft (OTFG-ultrasoft) pseudopotentials in CASTEP [5]. PBE-GGA was used as the functional. Convergence tests were performed on both cutoff energy and k-points. The lattice constant of a= 2.6 Å and c=4.1392 Å (smallest value) is used for the convergence test since the smaller lattice constant usually requires a larger k-point number and this can ensure all the calculations performed in this work converge. K-points are tested from 1 to 198 and values of cutoff energy vary from 100 eV to 600 eV. The result of energy to cut-off energy and k-points relation was shown in Figure 2 and Figure 3. The step energy difference (energy calculated in the current step subtract energy calculated in the last step) of two convergence tests was also calculated and has been shown in Figure 2 and Figure 3. The step energy difference was under 0.01eV when k points reached 144 (14*14*11) and under 0.001eV when cut-off energy reached 475 eV.

Figure 2 Energy and step energy difference versus the k-point number. K-point number of 1 and 2 is not shown in the main figure. Due to the large difference in both energy and step energy difference for k-point number small than 3, the whole picture is shown in the small figure.

Figure 3 Energy and energy difference versus cutoff energy.

Lattice constant calculation

K-point set of 14*14*11 and cutoff energy of 475eV are used to calculate energy corresponding to different lattice parameters ranging from a=2.6Å to a=3.7Å. The core radius for ultrasoft pseudopotential for Zr is 2.1 Bohr (~1.11 Å). The ultrasoft pseudopotential was generated with 12 valence electrons (4s2 4p6 4d2 5s2). The lattice parameter c is determined by the lattice constant ratio (c/a) 1.592 and the value of the lattice parameter a. The result of our calculation is shown in Figure 4. Lattice parameter corresponding to lowest energy (-2578.849923 eV) is a= 3.235 Å and c= 5.15012 Å. Compare to the measured lattice parameter at 4.2 K, our result is a little larger with an error of 0.17%. The calculated result is relatively closer to the experimentally observed data at room temperature, with an error of less than 0.1%. The small error in lattice constant value indicates the accuracy of our DFT calculation. The difference between our calculated result and experimental results may be due to the fact that we don’t know the “true exchange-correlation functional”. Choosing other functionals and performing more calculations may give a more accurate result.

Figure 4 Energy versus lattice constant for α-zirconium. The enlarged figure of the lowest energy point is shown in the small figure. Lattice constant corresponding to the lowest energy is ~3.235 eV.

References:

[1] Versaci, R. A., and M. Ipohorski. Temperature dependence of lattice parameters of alpha-zirconium. No. CNEA–500. Comision Nacional de Energia Atomica, 1991.

[2] Goldak, J., L. T. Lloyd, and C. S. Barrett. “Lattice parameters, thermal expansions, and Grüneisen coefficients of Zirconium, 4.2 to 1130 K.” Physical Review 144.2 (1966): 478.

[3] Easton, D. S., and J. O. Betterton. “The eutectoid region of the Zr− Ga system.” Metallurgical Transactions 1.12 (1970): 3295-3299.

[4] Schnell, I., and R. C. Albers. “Zirconium under pressure: phase transitions and thermodynamics.” Journal of Physics: Condensed Matter 18.5 (2006): 1483.

[5] Sholl, David, and Janice A. Steckel. Density functional theory: a practical introduction. John Wiley & Sons, 2011.

by Vishal Jindal

1. Introduction

Platinum (symbol Pt and atomic number 78) is a noble metal. It is used in catalytic converters, electrodes, and many other laboratory equipments, dentistry and jewelry [6]. Experimentally, platinum (Pt) is found to exist in cubic close-packed (ccp) structure with a lattice constant of a = 3.9242 Å [1]. In this post, we are using Density Functional Theory [DFT] [2] calculations to determine the preferred crystal structure for platinum metal amongst simple cubic (sc), cubic close-packed (ccp), also known as face-centered cubic (fcc) and hexagonal close packing (hcp) crystal structures.

2. Methodology

We used a plane-wave basis set with ultrasoft pseudopotentials as implemented in the CASTEP code [3] to perform DFT calculations to get total energy for different crystal structures and lattice parameters. Materials Studio was used as a builder, visualizer, and user interface for the CASTEP calculations. The exchange and correlation energies were calculated using the Perdew, Burke, and Ernzerhof (PBE) [4] functional described within the generalized gradient approximation (GGA) [5]. SCF tolerance is taken to be 2.0e-6 eV/atom for all the calculations. The “on the fly” generated ultrasoft pseudopotential for Pt has a core radius of 2.4 Bohr (1.27 Angstroms) and was generated with 32 electrons in the valence panel with (4f14 5s2 5p6 5d9 6s1) as the electronic configuration.

3. K-Points and Cut-off Energy Optimization

Before varying the lattice parameter to find the most stable crystal structure, we need to make sure that the plane-wave basis sets give convergent results for energies with respect to mesh size/ k-points and cut-off energy (ENCUT). To perform k-points and ENCUT optimization we used the experimental value of lattice parameter, i.e. a = 3.9242 Å.

3.1 K – Point Optimization

3.1.1 Simple Cubic (sc)

To optimize the k-points, we calculated total energy of simple cubic (sc) lattice for different mesh sizes (keeping ENCUT fixed at material studio default i.e. 272.1 eV). Fig. 1 shows the variation of total energy when we change the mesh size. We choose 8 x 8 x 8 lattice having 20 k-points as total energy changed less than 0.001 eV as we further increased the mesh size.

Figure 1. k-point optimization for simple cubic crystal lattice

3.1.2 Face-centered cubic (fcc)

Figure 2. k-point optimization for face-centered cubic crystal lattice

3.1.3 Hexagonal Close Packed (hcp)

Figure 3. k-point optimization for hexagonal close-packed crystal lattice

3.2 Energy cut-off

Now, using the optimized number of k-points from simple cubic, we varied ENCUT from 250-450 eV. Again, using the same convergence criterion of |ΔE| less than 0.001 eV on increasing the cut-off energy. In Fig. 4, we found that the energy cut-off of 425 eV sufficiently converged the total energy of the system. Similarly for FCC and HCP, 425 eV was taken to be the cut-off energy after checking the convergence of total energy at 400 eV, 425 eV, and 450 eV.

Figure 4. Total energy vs energy cut-off [ENCUT]. Total energy tends to converge at 425 eV.

4. Results

To optimize the lattice parameters, we minimize the total energy per atom (eV/atom) with respect to lattice constant (a) using respective k-points and energy cut-off for SC and FCC crystal lattice.

4.1 Simple Cubic (SC)

Figure 5. Total energy vs lattice parameter plot for SC

4.2 Face Centered Cubic (FCC)

Figure 6. Total energy vs lattice parameter plot for FCC

4.3 Hexagonal Closed Pack (HCP)

Figure 7. Total energy vs lattice parameter (a) plot for different values of c/a ratio along with trendlines connecting the same c/a ratio (c/a = 1.5, 1.67, 1.85)

5. Conclusion

The table below summarizes the optimized lattice parameter for all three types of crystal lattices studied in our report.

We can observe that among the three types of lattice structure listed above, the minimum total energy per atom is found to be for the Face Centered Cubic (FCC) crystal structure. Therefore, our DFT calculations show that the Platinum(Pt) crystal is most stable in the FCC lattice structure with a lattice parameter (a) of 3.97 Å. This is in line with the experimentally observed Face Centered Cubic (FCC) crystal structure of Platinum with a = 3.9272 Å.

6. References

[1] https://www.webelements.com/platinum/crystal_structure.html

[2] D. Sholl, J.A. Steckel, Density Functional Theory: A Practical Introduction, Wiley 2009

[3] J. Clark Stewart, D. Segall Matthew, J. Pickard Chris, J. Hasnip Phil, I.J. Probert Matt, K. Refson, C. Payne Mike, First principles methods using CASTEP,  Zeitschrift für Kristallographie – Crystalline Materials, 220(5-6) pp. 567-570 (2005)

[4] J.P. Perdew, K. Burke, M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 77 (1996) 3865-3868.

[5] J.P. Perdew, J.A. Chevary, S.H. Vosko, K.A. Jackson, M.R. Pederson, D.J. Singh, C. Fiolhais, Atoms, Molecules, Solids, And Surfaces – Applications of the Generalized Gradient Approximation for Exchange and Correlation, Phys. Rev. B, 46 (1992) 6671-6687.

[6] https://en.wikipedia.org/wiki/Platinum

Lingjie Zhou

Abstract

In this post, optimal lattice parameters of gold(Au) are analytically derived using Density Functional Theory(DFT) methods. Plane-wave basis set, pseudopotential DFT methods are used to calculate the energy dependence in Simple Cubic(SC), Face Centered Cubic(FCC) and Hexagonal Closest Packed(HCP) lattice system. The convergence of cutoff energy and the number of k points is also checked in this post.

Introduction

As well known, Au has a preferred lattice structure under Standard Temperature and Pressure(STD), which is FCC lattice with a=4.08Å. Single crystal gold is a good conductor and material for research purposes. Its good electronic properties make it one of the best platforms to conduct STM research. To predict which lattice structure is preferred, we need to compare the energy in different lattice structures. DFT can calculate the energy of the structures that don’t exist in nature, thus making it a powerful method to determine the optimal lattice structure theoretically. This can also enable us to predict the properties of materials that may not be normally present in experiments.

Methods:

The CASTEP[2] package is used to carry out the DFT calculation. The exchange-correlation functional is GGA-PBE. The ‘on the fly’ generated ultrasoft pseudopotential for Au has a core radius of 2.4 Bohr(1.27 Angstroms) and was generated with 32 electrons in the valence panel with (4f14 5s2 5p6 5d10 6s1) as the electronic configuration.

A kpoint set of 5×5×5 and cutoff energy 700eV is used to calculate the energy of SC and FCC lattice at different lattice parameters, while 10×10×5 kpoint mesh and 700eV cutoff energy is used for HCP lattice. The number of kpoint and cutoff is initially hypothesized as sufficient before checking convergence and the convergence will be further checked.

Figure 1 Lattice parameter optimization.a)SC using 5×5×5 kpoints and 700 eV cutoff energy 5b)FCC using 5×5×5 kpoints and 700 eV cutoff energy c)HCP using 10×10×5 kpoints and 700 eV cutoff energy

The SC lattice has its minimum energy at a=2.75Å, with E=-4.656eV. FCC lattice has its minimum energy at a=4.14 Å, with E= -5.12eV. For HCP lattice, there are two variables a and c. For fixed a/c ratio[1], the DFT can give the optimal a for the minimum energy. By comparing the minimum energy corresponding to different a/c ratio, HCP lattice has its minimum energy at a=2.91Å, a/c=1.68, with energy E=-5.018eV. Thus, the optimal lattice with these cutoff energy and kpoint choices is FCC lattice with a=4.14Å.

Cutoff energy test

The convergence of cutoff energy is tested using kpoint 5×5×5(a=2.75Å for SC and a=4.14 Å for  FCC), 10×10×5(a=2.91Å, a/c=1.68 for HCP).

Figure 2 Convergence test for the cutoff energy. a) SC with 5×5×5 kpoints, a=2.75Å b)FCC with 5×5×5 kpoints, a=414Å c) HCp with 10×10×5 kpoints, a=2.91Å, a/c=1.68

The total energy does not change more than 0.01eV beyond 400eV(SC), 500eV(FCC) and 400eV(HCP). So that the cutoff energy we used(700eV) is well satisfied.

Kpoint convergence test

After checking the convergence of cutoff energy, we need to make sure our calculation is also convergent under number of k points. Here we will check the kpoint convergence at the optimal values for the different lattices.

Figure 3 Convergence test for the kpoints. a) SC with a=2.75Å b)FCC with a=4.14Å c) HCp with  a=2.91Å, a/c=1.68. All with cutoff eneryg 700eV

The cutoff energy is 700eV for the kpoint convergence test. The energy is converged in the range of 0.01eV beyond 35 kpoints(9×9×9) for SC, 110 kpoints(10×10×10) for FCC and 120(16×16×8). The well converged total energy is -4.8149 for SC (a=2.75Å, 9×9×9, 700eV), -5.0174eV for FCC(a=414Å, 10×10×10, 700eV) and -5.011eV for HCP(a=2.91Å, a/c=1.68, 16×16×8, 700eV).

Conclusion:

The lowest energy phase of Au crystal was calculated to be FCC lattice structure with a=4.14Å. The experimental result is 4.08Å in FCC lattice structure[3], which is slightly smaller than the lattice parameters calculated.

Reference:

Author: Fan Zhang

Introduction

Ruthenium (Ru) is a rare transition metal with 44 electrons. According to experimental data, the preferred crystal structure of Ru is hexagonal closed pack (hcp) with a=270.59pm, b=270.59pm, c=428.15pm, \(\alpha\) = \(90.000^{\circ}\),  \(\beta\) = \(90.000^{\circ}\), \(\gamma\) = \(120.000^{\circ}\)[1]. This work aims at testing the preferred crystal structure of Ruthenium among simple cubic, face centered cubic (fcc) and hexagonal closed pack (hcp), as well as the preferred lattice constant in each structure by comparing the calculated energy of each configuration.

Method

The code used to calculate energy of various configurations is implemented by plane-wave density functional theory in CASTEP. The exchange-correlation functional used in the following calculations is Generalized Gradient Approximation (Perdew-Burke-Ernzerholf). The pseudopotentials used is OTFG ultrasoft which treats 4s 4p 4d 5s electrons in Ru as the valence electrons with a partial core correction of  \(r_c\)=59.4067pm. The self-consistent-field tolerance of the calculated energy is \(2^{-6}\) eV. K points sampling used in the calculation is 20x20x20 (220 irreducible k points in total with a density around 0.0142/\(nm^3\)) for simple cubic lattice, 14x14x14 (280 irreducible k points in total with a density around 0.0158/\(nm^3\)) for fcc lattice, 16x16x11 (180 irreducible k points in total with a density around 0.0197/\(nm^3\)) for hcp lattice. The cut off energy is 550eV for all cases. The convergence of both k points sampling and cut off energy were achieved with  \(\Delta\) E \(\leq\) 0.01eV. The convergence of the found k points sampling and cut off energy are rechecked in each case.

Result

1.Initial convergence of cut off energy

The convergence of cut off energy is done by using the bravais lattice of hcp crystal of Ru. The k points configuration used is 9x9x6 mesh as default. Data can be seen in Table 1. The highlighted row is the cut off energy chosen for the following calculation. The energy difference after this value is \(\leq\) 0.01eV. The corresponding graph of these data is also shown in Figure 1. In the following calculation, the cut off energy will be fixed at 550eV to allow for the comparison between different structures [2].

Table.1 initial convergence of cut off energy

Fig.1 initial convergence of cut off energy

2.Initial convergence of k points

With the chosen cut off energy (550eV) and the same crystal structure, the convergence of k points sampling was done and the data are shown in Table 2 and Figure 2. According to the data, 16x16x11 (with the k points density equals 0.0197/\(nm^3\)) was chosen as the reasonable sampling configuration. In the following calculation, the k points density was kept around 0.0197/\(nm^3\) and the convergence energy tolerance was kept around 0.005eV to allow for the comparison between different structures [2].

Table.2 initial convergence of k points sampling

Fig.2 initial convergence of k points sampling

3.Simple cubic structure

The crystal structure used here is a=b=c=lattice constant,  \(\alpha\) = \(\beta\) = \(\gamma\) = \(90.000^{\circ}\). One Ru atom is put on site (0, 0, 0). The lattice constant was varied from 2.43A to 2.6A. Energy per unit cell, the energy difference between successive calculations and k points density of each case were calculated. Data and the corresponding plot is shown in Table 3 and Figure 3.

Table.3 optimization of simple cubic lattice

Fig.3 optimization of simple cubic lattice

By doing a quadratic fitting of the data points near the bottom of the curve as shown in Figure 4, the most preferred lattice constant is calculated as 2.5100A with an energy 1.172eV per unit cell relative to the optimal energy for hcp lattice. (The calculation for hcp lattice was first done to give this optimal energy.)

Fig.4 fitting of simple cubic lattice optimization

The convergence of cut off energy and k points sampling are also confirmed as shown in Table 4 and Table 5. The level of convergence are clearly the same as the initial convergence.

Table.4 check for cut off energy convergence

Table.5 check for k points sampling convergence

4.Face centered structure

The crystal structure used here is a=b=c=lattice constant,  \(\alpha\) = \(\beta\) = \(\gamma\) = \(90.000^{\circ}\). Four Ru atoms are put on site (0, 0, 0), (0, 1/2, 1/2), (1/2, 0, 1/2) and (1/2, 1/2, 0) separately. The coordinates are given as a fraction of the corresponding lattice vector. The lattice constant was varied from 3.72A to 3.9A. Energy per unit cell, the energy difference between successive calculation and k points density of each case were calculated. Data and the corresponding plot are shown in Table 6 and Figure 5.

Table.6 optimization of fcc lattice

Fig.5 optimization of fcc lattice

By doing a quadratic fitting of the data points near the bottom of the curve as shown in Figure 6, the most preferred lattice constant is calculated as 3.8093A with an energy of 0.059eV per unit cell relative to the optimal energy for hcp lattice. (The calculation for hcp lattice was first done to give this optimal energy.)

Fig.6 fitting of fcc structure optimization

The convergence of cut off energy and k points sampling were also confirmed as shown in Table 7 and Table 8. The level of convergence are clearly the same as the initial convergence.

Table.7 check for cut off energy convergence

Table.8 check for k points sampling convergence

5.Hexagonal closed pack structure

The crystal structure used here is a=b=lattice constant, c=ax1.5823,  \(\alpha\) = \(\beta\) = \(90.000^{\circ}\),  \(\gamma\) = \(120.000^{\circ}\). One Ru atom was put on site (0, 0, 0) and another Ru atom was put on site (2/3, 1/3, 1/2). The coordinates are given as a fraction of the corresponding lattice vector. The lattice constant was varied from 2.63A to 2.8A. Energy per unit cell, the energy difference between successive calculations and k points density of each case were calculated. Data and the corresponding plot are shown in Table 9 and Figure 7.

Table.9 optimization of hcp lattice

Fig.7 optimization of hcp lattice

By doing a quadratic fitting of the data points near the bottom of the curve as shown in Figure 8, the most preferred lattice constant is calculated as 2.7181A with an energy 0eV per unit atom relative to the optimal energy for hcp lattice. (The calculation for hcp lattice was first done to give this optimal energy.) One unit cell contains two atom in this case thus the energy has to be divided by 2 to give the energy per atom. The experimental result for this lattice constant is 2.7059A.

Fig.8 fitting of hcp structure optimization

The convergence of cut off energy and k points sampling are also confirmed as shown in Table 10 and Table 11. The level of convergence are clearly the same as the initial convergence.

Table.10 check for cut off energy convergence

Table.11 check for k points sampling convergence

Conclusion

By comparing the energy per atom calculated above as shown in Table 12, it is clear that hcp is the most preferred crystal structure. This observation agrees with the experimental result. The calculated preferred value  and experimental value for the lattice constant are different by only 0.45% which indicates the high reliability of the calculation.

Table.12 Comparison of deferent structures

References

Introduction

Bulk hBN (30-50nm thick, for example) is often used in modern research to make heterostructures and its lattice constants are very useful information to researchers in considering lattice mismatch and strains. Hereby density functional theory (DFT) calculations are performed to numerically solve for the optimal lattice constants (a and c) of hBN, which are then compared with the experimental values. The experimental optimal values for a/b axis are 2.502Å, and for c it is 6.617Å [1]. The specific code package used to perform the calculations is the Cambridge Serial Total Energy Package (CASTEP), which uses a plane-wave basis set. The functional used to perform the calculations is GGA-PBE. hBN is not a metal and does not have spin-orbit coupling or spin-polarization. On the fly generated (OTFG) ultrasoft pseudopotential is used for the calculations.

An illustration of the hBN unit cell

Calculation Results and Discussions

The convergence test is initially performed using a=2.50Å and c=6.62Å and then calculations with large step size are performed. Surprisingly, the energy as a function of c is minimized at around 8.55Å, which is much larger than the experimental value (6.62Å).

It turns out that it is not considering the dispersion correction that caused this problem. Noncovalent forces such as van der Waals interaction play a crucial role in the formation of layered materials such as hBN. However, the noncovalent forces are not easy to be accounted for in calculations and are ignored in the local density approximation (LDA) and generalized gradient approximation (GGA) functionals. Therefore when performing calculations without dispersion corrections, the interlayer interaction is weaker due to the absence of van der Waals interaction and the preferred value of c is larger. Luckily, many semiempirical solutions have been developed regarding this problem. To better demonstrate the importance of the dispersion corrections, here the calculation results are reported in two parts, with the first part not using the TS method (one semiempirical dispersion correction that works well for GGA-PBE functional) and having preferred c around 8.55Å as result and the second part using the TS method and having preferred c close to the experimental value as result.

I. Finding the optimal value of c without dispersion corrections

Since the results from calculations without dispersion corrections are not precise in the first place, the report of the convergence test is skipped here. A k-point mesh of 9 by 9 by 4 and an energy cutoff of 600 eV should be fine enough for the purpose of demonstrations. With a=2.50Å and a step size of 0.3Å, the optimal value of c is found to be around 8.55Å with an error range of 0.15Å (since the smallest two energies are with c=8.4Å and c=8.7Å, the optimal value of c must be within the interval from 8.4Å  to 8.7Å), which is a very coarse calculation in terms of error range, but it is good enough to show that the optimal value of c without the consideration of dispersion corrections is much larger than the experimental value.

The total energy versus the value of c

II. Finding the optimal values of a and c with dispersion corrections

II. i. Convergence test

Using a=2.50Å and c=6.62Å, the convergence test is performed on k-points and the energy cutoff. The TS method is used for dispersion correction. SCF tolerance is chosen to be medium. The valance electron configuration of B is 2s2 2p1, with partial core correction Rc = 0.838 Bohr radius. The valance electron configuration of N is 2s2 2p3, with partial core correction Rc = 0.769 Bohr radius.

The convergence test on k-points is first performed. An energy cutoff of 600eV should be enough for the purpose of this test. It turns out that within the precision of 0.0001eV, the energy converges very quickly and the choice of the k-points mesh can be rather arbitrary, with the choices of 8/9/10 by 8/9/10 by 3/4/5. A mesh of 9 by 9 by 4 is chosen for later calculations.

Then a proper energy cutoff needs to be decided. A series of calculations is performed, with the cutoff energy begins at 400eV and increases with steps of 50eV. Since the energy monotonically decreases with the increase of the cutoff energy, the total energy will never converge. But a cutoff that is good enough can be determined by calculating the difference between each total energy. And the magnitude of the difference in total energy monotonically decreases with the increase of the energy cutoff.  In this way, the change in energy versus the cutoff energy can be plotted and 800eV is good enough for later calculations since the change in total energy is only -0.0004eV when cutoff energy increases from 750eV to 800eV.

The change in total energy due to the increase of cutoff energy versus the cutoff energy

II. ii. Finding the optimal value of c coarsely

With the value of a/b axis fixed at 2.50Å and a step size of 0.20Å for c, the optimal value of c is coarsely found to be around 6.70Å with an error range of 0.10Å, which is much closer to the experimental value (6.617Å) compared with the optimal value from the calculations without the consideration of the dispersion corrections (8.55Å). The plot of the total energy versus the value of c is as follows:

The total energy E (eV) versus the value of c (Å). The smallest two energies are found at c=6.60Å and c=6.80Å. Therefore the optimal c must be within that interval.

II. iii. Finding the optimal values of a/b and c finely

The step size in a/b direction and in c direction is 0.02Å and 0.05Å respectively.

The values in the first column are the values of a/b used in the corresponding calculations, and the values in the first row are the values of c used in the corresponding calculations. The lower right 5 by 5 corner of the table are the corresponding calculated energy results.

It can be seen from the table that for each different c, the optimal value of a/b is always 2.51Å plus or minus 0.01Å. This agrees really well with the experimental value (2.502Å), with only 0.32% off.

However, for different values of a/b, the optimal c is different. For a/b=2.46Å and 2.48Å, the optimal c is 6.575Å plus or minus 0.025Å, which is 0.63% off the experimental value (6.617Å). And for a/b=2.50Å, 2.52Å, and 2.54Å, the optimal c is 6.625Å plus or minus 0.025Å, which is 0.12% off the experimental value (6.617Å).

0.63% and 0.12% are both reasonably good. But it is not hard to notice that the total energy is more sensitive to the change in a/b axis than the change in c axis, with ΔE due to 1% change in a/b is in the order of 0.01eV whereas ΔE due to 1% change in c is in the order of 0.001eV. A possible explanation is that the semiempirical dispersion correction potential is proportional to , whereas the in-plane potential is proportional to , and therefore the energy is more sensitive to the in-plane lattice change.

The energy versus a/b at different values of c. It is easy to read from the plot that the change in energy due to a/b is much larger than the change in energy due to c which is barely readable from the plot.

Conclusion

The optimal lattice constants given by the CASTEP calculations are a/b=2.51Å plus or minus 0.01Å which is 0.32% off the experimental value (2.502Å), and c=6.625Å plus or minus 0.025Å which is 0.12% off the experimental value (6.617Å). The numerical results agree well with the experimental values and provide a good demonstration of how powerful DFT calculations can be.

References

1. http://www.hqgraphene.com/h-BN-CAN1.php

Author: Jeremy Hu

Introduction

Silver (Ag) has been used for multiple chemical engineering applications, most notably in the field of catalysis. In fact, Ag catalysts are used in a wide field of applications including electrocatalysis and oxidation/reduction reactions due to their high activity and stability [1]. Understanding the crystal structure of Ag may aid in explaining the structure and behavior of Ag in various applications.  Experimental studies on the crystal structure of Ag suggest that Ag prefers the fcc crystal structure with a lattice constant of a = 4.079 Å [2]. To offer a comparison to the experimental data on Ag, plane-wave density functional theory (DFT) was used to characterize and optimize three crystal structures of Ag using CASTEP in Materials Studio [3]. The structure and energy of Ag in simple cubic (sc), face-centered cubic (fcc), and hexagonal close-packed (hcp) crystal structures were analyzed [4].

Methods

Electronic Methods

DFT analysis of Ag was run using the plane-wave basis set in CASTEP in Materials Studio using the following parameters:

Table 1. Parameters for DFT Calculations in CASTEP

First, the energy of the sc, fcc, and hcp crystal structure of Ag was iterated with respect to the energy cutoff (ENCUT) and the irreducible number of k-points. The energy cutoffs and irreducible number of k-points were considered converged when the energy did not vary significantly from the energy at the infinite energy cutoff or irreducible k-point limit (i.e., the energy at the highest ENCUT or number of k-points). For each convergence check, the relative energy was reported with respect to the energy value at the highest number of irreducible k-points or ENCUT. For the initial convergence check for the minimum number of irreducible k-points, the default ENCUT in CASTEP of 489.8 eV was used. The assumption that the default ENCUT was high enough to ensure convergence was confirmed during the ENCUT convergence check.

After a minimum ENCUT and irreducible number of k-points were identified (i.e., the values at which the energy was considered converged), lattice parameters were varied for three different crystal structures of Ag (e.g., sc, fcc, and hcp) and the relative energy was plotted as a function of the lattice parameters. The energy minimum of each plot corresponds to the preferred (i.e., energetically favorable) lattice parameter.

Model

Crystal structures of Ag were tested with the following parameters:

Table 2. Iteration ranges of parameters for three possible crystal structures of Ag

Results and Discussion

1. K-point convergence

The energy of Ag in the sc structure was converged after 20 irreducible k-points, with the relative energy reaching within 0.01 eV/atom (Fig. 1).

Figure 1. Relative energy (eV/atom) as a function of irreducible k-points for the simple cubic (sc) structure of Ag at a = 2.7 Å and ENCUT = 489.8 eV.

Next, the energy of the fcc structure of Ag was converged after 28 irreducible k-points, where the relative energy was less than 0.01 eV/atom than the energy at the infinite k-point limit (Fig. 2).

Figure 2. Relative energy (eV/atom) as a function of irreducible k-points for the face-centered cubic (fcc) structure of Ag at a = 4.1 Å and ENCUT = 489.8 eV.

Finally, the energy of the hcp structure was converged after 216 irreducible k-points, with a relative energy of 0.007 eV/atom (Fig. 3).

Figure 3. Relative energy (eV/atom) as a function of irreducible k-points for the hexagonal close-packed (hcp) structure of Ag at a = 2.8 Å, c/a = 1.7, and ENCUT = 489.8 eV.

For the purposes of brevity, it is assumed that the irreducible k-points necessary for convergence at the chosen arbitrary lattice constants is valid for lattice constants close to the chosen values.

2. Cutoff energy convergence

The energy of the fcc structure was determined at various cutoff energies from 200 eV to 600 eV. The minimum cutoff energy was 450 eV, where the corresponding energy had less than a 0.1% difference than the energy at the highest cutoff energy (Fig. 4). Since the cutoff energy should be kept constant for all the crystal structures for optimization, it was assumed that the same minimum cutoff energy would be appropriate for the other crystal structures.

Additionally, Fig. 4 confirms the assumption that the default ENCUT value of 489.8 eV used for the previous k-points convergence was sufficient to ensure convergence with respect to the ENCUT value.

Figure 4. Relative energy (eV/atom) as a function of cutoff energy for the face-centered cubic (fcc) structure of Ag at a constant 10 x 10 x 10 Monkhorst k-point grid (i.e., 110 irreducible k-points) and a = 4.1 Å.

3. Lattice parameter optimization

In the following lattice parameter optimization calculations, the lattice parameter (a) was varied for each structure. Each energy value was taken relative to the lowest calculated energy in the most stable structure.

For the sc structure of Ag, the energy minimum was observed at around a = 2.7 Å (Fig. 5), which corresponds to a minimum relative energy of 0.325 eV/atom.

Figure 5. Relative energy (eV/atom) as a function of lattice parameter (Å) for the simple cubic (sc) structure of Ag at a constant 10 x 10 x 10 Monkhorst k-point grid and ENCUT = 489.8 eV.

Since the hexagonal close-packed structure of Ag has two lattice parameters (i.e., a and c), the ratio of c/a was kept fixed from c/a = 1.5 – 1.7 for each iteration of a. The relative energy minimum was found to be 0.237 eV/atom at a = 2.8 Å and c/a = 1.7 (Fig. 6).

Figure 6. Energy (eV/atom) as a function of lattice parameter (Å) for the hexagonal close-packed (hcp) structure of Ag at a constant 12 x 12 x 6 Monkhorst k-point grid and ENCUT = 489.8 eV.

Finally, iterations were performed for the fcc structure of Ag, where the lowest energy out of all systems (i.e., the state where the relative energy was set to zero) was observed at a = 4.1 Å (Fig. 7).

Figure 7. Energy (eV/atom) as a function of lattice parameter (Å) for the face-centered cubic (fcc) structure of Ag at a constant 10 x 10 x 10 Monkhorst k-point grid and ENCUT = 489.8 eV.

Conclusion

The convergence checks for each crystal structure with respect to k-points and cutoff energy confirm that the values of irreducible k-points and ENCUT used in the crystal structure calculations were converged with respect to energy. The final parameter values for each crystal system is shown below in Table 3.

Table 3. Final lattice parameters and parameter values for Ag in the sc, fcc, and hcp crystal structures.

Thus, our DFT calculations suggest that Ag prefers the fcc crystal structure with a lattice parameter of a = 4.1 Å since it has the minimum energy (i.e., the most thermodynamically favorable crystal structure).  These results are consistent with the experimentally determined results, which show that Ag exists as the fcc crystal structure with a lattice constant of a = 4.079 Å [2]. These results on the crystal structure of Ag are promising for understanding Ag-based catalysts, such as catalysts with Ag nanoparticles.

Citations

[1] G. Liao, J. Fang, Q. Li, S. Li, Z. Xu, B. Fang, “Ag-Based nanocomposites: synthesis and applications in catalysis,” Nanoscale, 2019, 11, 7062-7096
[2] W. Davey, “Precision Measurements of the Lattice Constants of Twelve Common Metals,” Physical Review, 1925, 25 (6), 753-761.
[3] Clark Stewart J et al., “First principles methods using CASTEP ,” Zeitschrift für Kristallographie – Crystalline Materials, 2005, 220, 567
[4] D. Sholl, J. Steckel, “Density Functional Theory,” Somerset: Wiley, 2008
[5] J. P. Perdew, K. Burke, M. Enzerhof, “Generalized Gradient Approximation Made Simple,” Phys, Rev. Lett., 1996, 77, 3865.
[6] H. J. Monkhorst, J.D. Pack, “Special points for Brillouin-zone integrations,” Physical Review B, 1976, 13, 5188-5192.

Introduction

Iron (Fe) is known to have a bcc crystal structure at temperatures lower than 1100 K [1]. Its optimal lattice parameters for this structure are derived using Density-Functional Theory (DFT) methods. The Cambridge Serial Total Energy Package (CASTEP) software package, which uses plane-wave basis sets in order to analyze crystal structures, is implemented to analyze the bcc lattices of Fe to determine the optimal parameters. Two functionals in the generalized gradient approximations, PBE and PW91, are used to derive these parameters. The PBE and PW91 functionals are expected to produce virtually identical results [2]. A comparison between the results obtained from these functionals is made along with the computational costs associated with both of them.  

Methodology 

We use the plane wave DFT calculations to evaluate the optimal lattice parameter for Fe bcc crystal structure. All the calculations were performed using the CASTEP Simulation Package in Material Studio. The exchange and correlation energies were calculated using the PBE and the PW 91 functional described within the generalized gradient approximation (GGA). Electronic convergence tolerance of 2E-06 was used for all the calculations. The core electrons were treated using “on the fly” generated (OTFG) ultra-soft pseudo-potential with a core radius of 2.4 Bohrs (1.27 Angstrom) generated with a panel of 8 valence electrons ( 3d6 4s2). All the calculations are performed with the spin-polarized option ON as Fe is a magnetic element. 

Cut-off Energy and K-Point Optimization 

The essential step before performing a plane-wave basis set is to optimize the k-points and cut-off energy. This process is performed with both the functionals. 

K-point  

Fig.1 K-point convergence for PW91 functional. The Y-axis is the energy difference between successive calculations. The red line represents the convergence criteria.

Fig. 2 K-point convergence for PBE functional. The Y-axis is the energy difference between successive calculations. The red line represents the convergence criteria.

The experimentally determined optimal lattice parameter for Fe bcc crystal structure is 2.856 Angstrom [1]. However, it is more appropriate to perform k-point optimization on the lowest lattice dimension being investigated. As the smallest lattice parameter in real space gives the longest parameter in k-space. Hence the K-point optimization is performed at the lattice parameter of 2.3 Angstrom. A very high cut-off energy value is selected here 500 eV to avoid its effects on k-point optimization.

Table 1: K-point grid vs the number of K-points used

Figs.1 and 2 show the absolute change in the consecutive total energy (|ΔE|) with respect to the number of irreducible k-points. The corresponding K-point grid is shown in Table 1. As a convergence criterion of |ΔE| less than 0.04 eV is used for both the functionals. This corresponds to the optimal grid of 9x9x9. 

Cut-off energy 

Fig. 3 Cut-off energy convergence for PW91 functional. The Y-axis is the energy difference between successive calculations. The red line represents the convergence criteria.

Fig. 4 Cut-off energy convergence for PBE functional. The Y-axis is the energy difference between successive calculations. The red line represents the convergence criteria.

In Figs. 3 and 4, the absolute change in the consecutive total energy (|ΔE|) is plotted as a function of the cut-off energy. As a convergence criterion, it is assumed that the total energy is converged if |ΔE| is less than 0.03 eV. From Figs. 3 and 4, it is clear that the cut-off energy of 400 eV sufficient considering both the functionals. A lattice parameter of 2.856 Angstrom and K-point grid of 9x9x9 is used for this convergence. 

Fe lattice optimization 

To optimize the Fe bcc lattice parameter, the crystal structure energy is calculated for the bcc geometry while changing the lattice parameters from 2.3 to 3.5 angstrom with an interval of 0.1 Angstrom. Based on the K-point and cut off energy convergence study, cut-off energy of 400 eV and a K-point grid of 9x9x9 is employed in these calculations.  

Results

Fig. 5 shows the lattice parameter optimization. A curve is fitted to the DFT data to get an estimate of the energy minima with respect to the lattice parameter. A polynomial fit of order 4 is used for this purpose for data ranging from lattice parameter 2.6 to 3. Table 2 compares the optimum lattice parameters calculated using both the functionals. Both the functionals give optimum lattice parameter values close to the experimental data. There is hardly any difference between the values determined by both functionals. Table 2 shows the time required for calculations using both the functionals, which is not much different. 

Table 2: Results of calculations

Conclusions 

Density Functional Theory-based calculations are used to ascertain the lattice parameters of the Fe bcc crystal. It is determined by varying the lattice parameters and calculating their respective energies. The optimized lattice parameters obtained are reasonably coherent with the experimental results. A comparative study of the PBE and the PW91 functionals is also performed. It shows that both the functionals give very similar results while using similar computational time although PBE is a simplification of PW91 functional [2]. 

References

1. Greenwood, Norman Neill, and Alan Earnshaw. Chemistry of the Elements. Elsevier, 2012.
2. Mattsson, Ann E., et al. “Nonequivalence of the generalized gradient approximations PBE and PW91.” Physical Review B 73.19 (2006): 195123.

By Nate Klassen

Introduction

This project applies a method for confirming the lattice constant for crystalline silver (Ag).  The starting assumption is that the crystal has an FCC structure.  This is to reduce the scope of this investigation purely to the value of the lattice constant.  The structure is allowed to vary its volume, but the shape (FCC structure/ratio) is held constant.  The DFT calculations were run using CASTEP[1], OTFG ultrasoft pseudopotentials, the default GGA PBE Functional, and Koelling-Harmon “relativistic treatment.”  Ag has the electron configuration of 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s1, and the pseudopotential treats 4s2 4p6 4d10 5s1 as the valence electrons.  The Convergence tolerances were chosen somewhat arbitrarily to be small:  Energy at 1.0e-5 eV/atom, Force at 0.01 eV/Å, stress at 0.05 GPa, and displacement at 0.001 Å.  For all the rest of the options, the defaults were used.

Figure 1: The Ag structure, FCC single atom basis.

Results

1. Initial Guess

An initial automatic optimization using geometry optimization was run to get an initial value to use in further testing.  The experimentally known value for the lattice constant of Ag is 4.09 Å.[2]  Knowing this, the first chosen starting guess was 4 Å.  This first calculation was run with the default energy cutoff of 517 eV and a 7x7x7 k-point grid (24 k-points).  It achieved the convergence criteria after 4 steps and the lattice constant found was 4.201 Å.  This is approximately a 2% deviation from the true value.

2. Convergence Steps in Initial attempt

2. k-points

Using a fixed lattice parameter 4.20 Å, several different values for number of k points were tested against the energy to see which is the optimal choice. These calculations were run with the default energy cutoff of 517 eV.  The following results were found.

3. System energy as a function of k-points

4. Sampling size vs. number of k-points

From this data, it is clear that a grid size of 9x9x9 should be chosen.

3. Energy Cutoff

Next, calculations were run keeping the geometry fixed and k-points in a 9x9x9 grid with the energy cutoff value varied between 400 and 750 eV.  It is clear that at 600 eV, there is fairly good convergence.  Any cutoff greater than 600 eV is sufficient.  The convergence criteria for each of these values was 1.0e-5 eV/atom.

5. Energy Cutoff Analysis

4. Final Calculations

Lastly, calculations were run to optimize the lattice parameter.  The lattice parameter was fixed at various values and compared against the energy.  The lattice parameter that minimizes the energy is most likely to be correct.  An energy cutoff of 610 eV was used and a k-point grid of 9x9x9.

6. Energy vs. Lattice parameter

The energy reaches a minimum at 4.1 Å, which is an improved estimate in terms of accuracy to the true experimental result of 4.09 Å.

References

1.  “First principles methods using CASTEP” Zeitschrift fuer Kristallographie 220(5-6) pp. 567-570 (2005) S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson, M. C. Payne
2. https://periodictable.com/Elements/047/data.pr.html
3. Density Functional Theory: A Practical Introduction. (2009)  David S. Sholl, Janice A. Steckel

Author:

Mihir Parekh

Abstract:

In this project, ‘Material Studio’ has been used to study the crystal structure of lithium by using Density Functional Theory (DFT). Optimum lattice parameters have been obtained for BCC, SCC, and FCC lattices  by using plane-wave basis set density functional theory methods [1].  A comparison of 0 K lattice energies at the optimum lattice parameter suggests that the energy difference between BCC and FCC is lower than 0.005 eV, with BCC having lower energy. However, SCC has a significantly higher energy compared to BCC and FCC.

Introduction:

Lithium is a very important component of batteries today. Today, lithium ion batteries are being used in variety of applications such as electric vehicles, laptops, mobile phones, grid storage etc. and lithium metal batteries are amongst the most promising future energy storage technologies. Hence, lithium is one of the most important metals and so the crystal structure of lithium was studied in this project. Density Functional Theory (DFT) was used for studying the crystal structure as it is much cheaper than using experimental techniques such as X-ray diffraction. Moreover, repeating calculations in a software is also much cheaper than repeating an experiment.

Methods:

In order to study the crystal structure of lithium, energy was minimized for different crystal structures by using CASTEP in Material studio. For all calculations Generalized Gradient Approximation (GGA) and Perdew-Burke-Ernzerhof (PBE) exchange correlation functionals were used with On The Fly Generated (OTFG) ultrasoft pseudopotential. A core radius of 1 Bohr and an electronic configuration of 1s2 2s1 was used for calculations. Minimum energy of different crystal structures was compared to obtain the optimum crystal structure and the corresponding lattice parameter.

Fig. 1: Optimization of no. of k points

However, before varying the lattice parameter for a given crystal structure, the optimum number of k points and the cutoff energy to be used in calculations were obtained. The number of k points was optimized for BCC lattice with a lattice constant of 346 pm.  BCC lattice was chosen because at room temperature lithium crystallizes as BCC with a lattice constant of 351 pm [2]. Since 351 pm is the lattice constant of BCC at room temperature, varying the lattice constant from 346 pm to 356 pm would be sufficient to get an optimum lattice constant at which the energy is minimized. Moreover, lowest lattice constant requires the highest number of k points and hence 346 pm was chosen for optimizing the number of k points. Fig. 1 shows that a 12x12x12 grid in k-space is sufficient for an accuracy of  0.005 eV. The values plotted on y axis of Fig. 1 are the differences between energies of the current no. of k points and previous no. of k points. While optimizing number of k points, the cut-off energy was held constant at the default value of 408 eV.

Note: For Figs. 2,3,4,5 the energy values on y axis are relative to the lowest energy obtained during cutoff energy optimization.

Fig. 2: Cutoff energy optimization

Cut-off energy was then optimized for 12x12x12 grid on a BCC lattice with 346 pm as the lattice constant. Fig. 2 shows that a cutoff energy of 775 eV is good enough to obtain a roughly constant energy.  The difference between energies for a cutoff energy of 775 eV and 900 eV  is roughly 0.00057 eV. The energy difference for cut-off energy of 900 eV and 1000 eV is roughly 0.00056 eV. This shows is that the set tolerance criteria of 0.005 eV is satisfied if 775 eV is chosen as the cut-off energy.

Results:

For a fair comparison of the crystal energies, using a constant cut-off energy of 775 eV and a 12x12x12 grid in the reciprocal space, lattice parameters were varied for BCC, FCC and SCC lattices. However, for an SCC lattice a step change was seen in the energy vs lattice parameter plot. Hence, a higher cut-off energy of 1200 eV was used to obtain the optimum lattice parameters. The variation of energy versus lattice constant for BCC, SCC, and FCC lattices has been shown in Figs. 3, 4, 5 respectively. Thus, BCC with a lattice constant of 343 pm seems to have the least energy at 0 K. However, the difference between lowest energies of FCC and BCC is lower than the tolerance limit (0.005 eV) and hence it is difficult to distinctly predict the crystal structure. In Fig. 4 of their paper, Orlov et al. [3] mark a phase transition boundary for temperatures greater than 50 K. For any given pressure, Orlov et al. [3] predict FCC lattice at lower temperatures. So, the obtained result does not agree with the result reported by Orlov et al. [3].

Fig. 3: Lattice parameter optimization for BCC

Fig. 4: Lattice parameter optimization for SCC

Fig. 5: Lattice parameter optimization for FCC

Limitations:

1. Initially the number of k points were optimized for a lattice constant of 346 pm. However, clearly 346 pm is not the lowest amongst the various lattice constants used for BCC lattices. Thus. the number of k points used have not been optimized for the lowest lattice constant.
2. The cut-off energy and number of k-points were not optimized for FCC and SCC lattices.

References:

[1] Clark SJ, Segall MD, Pickard CJ, Hasnip PJ, Probert MI, Refson K, Payne MC. First principles methods using CASTEP. Zeitschrift für Kristallographie-Crystalline Materials. 2005 May 1;220(5/6):567-70.

[2] Mark Winter, U. (2020). WebElements Periodic Table » Lithium » the essentials. [online] Webelements.com. Available at: https://www.webelements.com/lithium/ [Accessed 31 Jan. 2020].

[3] Orlov AI, Brazhkin VV. Electron transport properties of lithium and phase transitions at high pressures. JETP letters. 2013 May 1;97(5):270-3.