Quick note on the 3D case. Setting the number of points as n, and labeling the three coordinate axes as

$$\{X, Y, Z\} \in \{1,…,n\}$$

Assuming X is {1,2,…,n}, the total number of permutations p possible for a fixed n is

$$p=n!^2$$

The number of permutations where all of the points are Pareto, i.e., nondominated, is the Sloane sequence A007767. The table below shows the first 13 values.

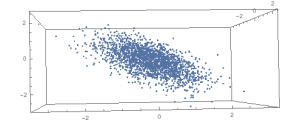
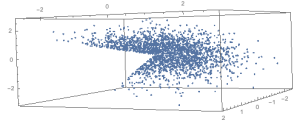
An interesting question is, given N Pareto points randomly distributed over the face of a simplex in d dimensions, what is the expected dominated hypervolume. This post builds up to an answer, starting with a block structure and moving to random data.

Block Data

Consider a block right pyramid in d dimensions. Here’s a 2D version, with side length = 4 and 10 blocks, and which also has 4 Pareto points.

And here’s a 3D version, again with side length = 4, but with 11 Pareto points and a dominated hypervolume of 20.

Here’s one more block pyramid, with the number of blocks along an edge = 15. It has a dominated hypervolume of 680 and the number of Pareto points (equal to the number of blocks on the face) is 120. In fact, the number of blocks on the face is just the d-1 dimensional problem of the number of blocks in the pyramid.

The outer corners all represent Pareto points. The dominated hypervolume is just the content of the pyramid, i.e., the number of blocks in the pyramid.

The generalized expression for the number of blocks in a pyramid of dimension d and with k blocks along an edge  is

Hypervolume

The number of blocks on a face is just the d-1 version of the above,

Pareto points = 

Unfortunately, there is no obvious smooth function that converts Pareto points into dominated hypervolume, as can be seen from some sample data from a 7 dimensional data set. We are stuck using the edge length as the independent variable. I threw the problem at Mathematica, but no joy.

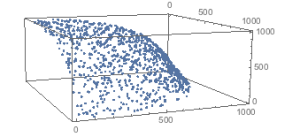
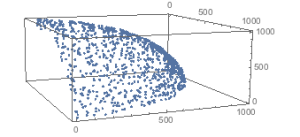
The interesting question is, what portion of a simplex is now dominated if we place the Pareto points on the outer face in this orderly fashion? The picture below shows a pyramid of edge length = 10, with the Pareto points highlighted and the enveloping simplex shown.

Given an edge length k and dimension d, the enveloping simplex has content of

Plotting the number of Pareto points versus portion of space dominated for a 7D space gives…

This shows that for a 7D simplex with 80,000,000 Pareto points evenly dispersed on the face, only 70% of the total simplex is dominated. Looking at a 15D example:

So in a 15 dimensional space with 80,000,000,000,000 points on the outer face, less than 20% of the total volume is dominated! Slow growth indeed.

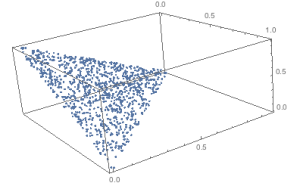
Random Data

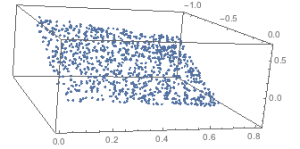
The block data is highly structured and you are restricted in the number of values Pareto points you can consider. To generalize, consider a simplex with points randomly distributed on the base facet of the simplex below.

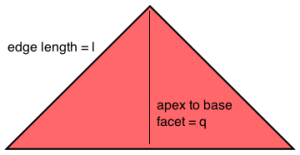
Label the shortest distance from the apex (top corner) to the base facet (the long edge on the bottom..the hypotenuse for the 2D case) as q. We can come up with an equation for the content c of the base facet as a function of q, and it is

Let \(\alpha=\frac{d^{d/2}}{d-1!}\)  to clean up the expression, so

Now to calculating the expectation of the dominated hypervolume of a simplex with dimension d, base distance q, and number of points N. What we will do first is compute the compliment, the expectation of the nondominated volume.

Pick a point that is a distance r from the base facet. You can construct a new simplex from this point with its base facet coincident with the orginal. The content of this new simplex’s base facet is .

If there are N points evenly spread on the base facet at distance r from the point of interest, we can compute the probability that none of them is within the area on the base facet, and so the point at r is nondominated.

Probability single random point falls in

$$\alpha r^{d-1}$$

is /(q^{1-d} r^{d-1}=\left(\frac{r}{q}\right)^{d-1}[/latex]\), so complementarily  the prob it does not fall in is

$$1-\left(\frac{r}{q}\right)^{d-1}$$.

Probability that all N points do not fall in is therefore

$$\left(1-\left(\frac{r}{q}\right)^{d-1}\right)^N,$$

and so probability that a point located distance r from the simplex base facet is non-dominated is

$$I(r)=\left(1-\left(\frac{r}{q}\right)^{d-1}\right)^N.$$

If we integrate this over all of the simplex  that is distance r from the base facet (this is of area =), we will get an expected amount of that face that is nondominated,

$$\alpha  I(r) (q-r)^{d-1}$$.

To get the expected total nondom content, integrate this over the range of r from 0 to q, and so over the entire volume of the simplex.

$$\int_{r=0}^q I(r) \alpha (q-r)^{d-1} dr  =\int_{r=0}^q\left(1-\left(\frac{r}{q}\right)^{d-1}\right)^N\alpha (q-r)^{d-1} dr $$

Change variables to simplify the integral a little. Let s = r/q, r = q s, ds = (1/q) dr, dr = q ds. Limits of integration are now 0 < s <1.

Nondominated volume = \(q^d \alpha \int_{s=0}^1\left(1-s^{d-1}\right)^N  (1-s)^{d-1} ds \)

The integral has no known (to me!) general solution, although Mathematica will slog through it for fixed values of N or d. The good news is Mathematica expeditiously numerically integrates it.

To look at ratios, we can compute the volume of the enveloping simplex similar to the blocks above, but using q as the independendent variable:

Volume of enveloping simplex = .

With this relationship and a little massaging, we can generate the following plot. Note how even with 400,000 points, in a 10D problem only 10% or so of the volume of the simplex is dominated.

We can compare the ratios computed by the block method at the top and the random method above. In the plot below, blue is the block results and gold is the random results. As expected, the block results more efficiently covers the volume. However, the two results converge as the number of Pareto points increases.

I’ve worked in the past on algorithms to approximate the hypervolume of data sets, but needed a way to generate some data sets to test the algorithms against. The algorithm to generate the data sets presented here does that, and also provides a way to generate data sets with known numbers of Pareto points as a byproduct.

The basics of the algorithm can be seen in this animation (click the graphic) which shows that new points are repeatedly created in the “corners” of the blocks. by doing this, we know exactly how much volume is added each time.

Here’s a partially constructed nest block.

And here is the Mathematica code to generate the data.

(MMA) Known HV for blog

Here’s the code in a PDF document.

(PDF) Known HV for blog

Most algorithms to identify the Pareto frontier don’t care about the actual values of the points, they only care about the order statistics. Are all of the attributes of one point at least as good as the attributes of another point, and is at least one better? If so, the first point dominates the second. Otherwise not.

So an interesting transformation of the data is to take each column of attributes, and replace their absolute values with a number that indicates their relative position in the ordering. So if we have three points that each have as attributes for max speed as {455, 22, 3090}, we replace those values with {2, 1, 3}. This retains their relative ordering. After doing this for each attribute, you end up with what I call Lattice Latin Hypercube form, or LLH for short. The Mathematica code to generate it is simple:

makeLLH[data_] := Transpose[Map[Ordering[Ordering[#]] &, Transpose[data]]];

Here are some examples of original data and transformed data.

Simplex data

Transformed

Notice how what was originally planar data is now convex. This was a surprise when I first saw it. Next example is spherical data.

Transformed.

Looks very similar. Next up is a rotated rectangular plane

Here’s a rotating GIF so you can see it is transformed from planar to…something otherwise. Click on the image to see it rotate, unable to do so in the post.

Here’s 4000 pts distributed multi-variate normal on a plane, and the transformed version. Significant difference!

Click on the plot to see a rotation.

If you are going to talk Pareto Frontier, you ought to know something about the simplex, in particular a right-simplex or orthogonal simplex. It is the simplest geometric figure you can construct in a particular dimensional space. There is of course a Wikipedia page full of useful information:

http://en.wikipedia.org/wiki/Simplex

What I will talk about here are the particular aspects that I find useful in analyzing Pareto Frontiers. First some definitions and laying out of terms.

So what exactly is a simplex? It is the simplest geometric figure possible within a particular dimensional space. This is a triangle in 2D space (three points), a tetrahedron in 3D space, and so on.

The geometric figure below is a trirectangular tetrahedron. The red face is referred to as the base facet, and the vertex opposite the base facet is the peak vertex. It is trirectangular because the three edges touching the base facet intersect at right angles to each other. For this case, the lengths of the edges that meet at the peak vertex are all the same length.

As noted, the d-dimensional generalization of a tetrahedron is the simplex. Referring to a simplex in d dimensions as a d-simplex, it will have d+1 facets, with each facet being a (d-1)-simplex itself. For example, the tetrahedron above is a simplex in 3D space, it has 3+1=4 facets, and each facet is a triangle, which is just a simplex in 2D space.

A d-dimensional simplex will be referred to as a d-rectangular simplex if all edges emanating from the peak vertex are orthogonal to each other, which is the case here. For this work, the lengths of the edges extending from the peak vertex are equal to each other, resulting in a higher dimensional analog to a right triangle referred to as a d-right simplex.

For labeling, we will refer to the edge length as l and the shortest distance from the apex to the base facet as q, as per the picture below.

The generalized term for the volume (3D) or area (2D) is the content. For a d-right simplex with orthogonal edges of length l, the content  c is

$$c=\int _0^l\int _0^{x_1}\int _0^{x_2}…\int _0^{x_{d-1}}dx_d…dx_3dx_2dx_1$$

or

$$c=\frac{l^d}{d!}$$

The relationship between edge length l and the distance q from the peak to the base facet is

$$q=\frac{l}{\sqrt{d}}$$

The generalized pythagorean theorem says that the square of the content of the base facet is the sum of the contents of the of the other (side) facets, and so

$$c_b^2=\sum _d c_s^2=d c_s^2$$

Since the content of the side facets is

$$c=\frac{l^{d-1}}{d-1!}$$

The content of the base facet is

$$c=\sqrt{d}\frac{l^{d-1}}{d-1!}$$

A little more massaging to get the area of the base facet in terms of q gives us

$$c_b=\frac{d^{d/2}} {d-1!}q^{d-1}$$

or defining the parameter α which is only a function of d:

$$\alpha _d=\frac{d^{d/2}}{d-1!}$$

We end up with the final version…

$$c_b=\alpha _d q^{d-1}$$

With this information, we can reason about relationships between clouds of Pareto points on the base facet and their dominated hypervolume. This, for a future post.

OK, experimenting with how to make blog entries, and also providing some information on how to generate points that are all Pareto optimal but are otherwise as random as possible. I created these methods back in 2004 while working on my PhD thesis. Since then, they’ve been recreated many times over, and one can google on them and get lots of hits. Here’s a useful page.

http://stackoverflow.com/questions/3010837/sample-uniformly-at-random-from-an-n-dimensional-unit-simplex

The algorithm to generate points on a simplex

Here’s a picture of 1000 points in 3 dimensions.

Here’s the code. If you cut and paste this into Mathematica, you may need to delete and retype the “d-1” term, as some sort of hidden formatting seems to carry over and mess up the evaluation when I try it.

genSimplex[n_, d_] := Table[Differences[Sort[Flatten[{0, RandomReal[1, d – 1], 1}]]], {n}];

The algorithm generates points that are randomly distributed on an outer face of a simplex. The way to generate them is, for a d-dimensional problem…

1. Generate d-1 uniformly distributed random values in the range [0,1]
2. Add a 0 and a 1 to the list
3. Sort the list
4. Extract a list of the differences between the elements

You now have a list of random values that sum to 1 (so they are on a plane that is defined by points that sum to one) and that are otherwise independent of each other, so their dispersion is uniform.

Generating Points on Hypersphere

This algorithm uses the fact that multivariate normal points distributed with \[Mu] = {0,…,0} and \[CapitalSigma] = Identity Matrix are uniformly sprayed out in all directions. So generate the points, take the absolute value of the coordinate values to move them all to the positive quadrant, and then normalize them to project them onto the unit hypersphere.

genSphere[n_, d_] := Table[Normalize[Abs[RandomVariate[MultinormalDistribution[ConstantArray[0, d], IdentityMatrix[d]]]]], {n}]

Picture of 1000 pts in 3D, with the aspect ratio a little squashed.

Generating Points on a Plane And Then Rotating Them

This algorithmic approach first generates points that form a d-1 dimensional cloud embedded in d dimensions, so each point has value [0  x1  x2 …. xd]. Thus the points are on a plane orthogonal to a d-dimensional vector [1  0 …. 0]. We next create a rotation matrix that will rotate the vector to [1 1 1 …. 1], and orthogonalize it. We then just multiply each of the data points by this matrix.

First example is generating a could that is distributed uniformly over a d-1 hypercube.

genRotatedPlane[n_, d_] := Map[Transpose@Orthogonalize@ReplacePart[IdentityMatrix[d], {1, i_} -> 1].# &, Transpose@Prepend[RandomReal[1, {d – 1, n}], Array[0 &, n]]];

You may need to retype sections in case some odd hidden formatting carries through. Example data set, 1000 pts in 3D.

Similar to above, but rather than generating a d-1 hypercube, we generate a d-1 multi-variate normal cloud with μ = [0 0 … 0] and Σ as the identity matrix. Lots of other potential approaches to generating the initial data prior to rotation.

genRotatedPlaneNormal[n_, d_] :=
Map[Transpose@Orthogonalize@ReplacePart[IdentityMatrix[d], {1, i_} -> 1].# &, Transpose@Prepend[RandomVariate[NormalDistribution[], {d – 1, n}], Array[0 &, n]]];

Here’s a modification that removes a chunk of the data.

genRotatedPlaneNormalChunkMissing[n_, d_] :=
Map[Transpose@Orthogonalize@ReplacePart[IdentityMatrix[d], {1, i_} -> 1].# &,
Select[Transpose@Prepend[RandomVariate[NormalDistribution[], {d – 1, n}],
Array[0 &, n]], ! AllTrue[#, NonPositive] &]];