Author: Sharad Maheshwari
Introduction
Surface diffusion can play an important role in creating a topological modification on the surface as in the case of nanoparticle growth. In the following work we aim to identify the kinetic barrier for the diffusion of a Silver (Ag) atom as it hops from a three-fold fcc site to the adjacent three-fold hcp site on (111) surface of Copper (Cu). We will use density functional theory-based methods to evaluate the activation barrier for the hopping process. We will also calculate the frequency of this hopping process.
Calculation Details
Electronic Calculations
Electronic structure calculations were performed using the Vienna Ab initio Simulation Package (VASP)[1, 2] a plane wave basis set pseudo-potential code. We used the projector augmented wave (PAW) [3] method for core-valence treatment. The exchange and correlation energies were calculated using the Perdew, Burke, and Ernzerhof (PBE) [4] functional described within the generalized gradient approximation (GGA) [5]. A plane-wave basis set cutoff energy of 450 eV was used. The ionic convergence limit was set to 0.01 eV Å-1 while the electronic convergence limit was set to 10-5 eV. The Fermi level was smeared with the Methfessel-Paxton [6] scheme using a smearing width (σ) of 0.2 eV.
Surface Model
A 3 x 3 surface slab model was used to construct periodic surfaces of Cu (111) using an experimental bulk lattice constant of 2.556 Å. The slab models were comprised of 4 layers of metal atoms. The top two layers of the slab along with the adsorbate were allowed to relax until the force on atoms in these layers was within 0.01 eV Å-1 while the bottom two layers were kept fixed to imitate their bulk arrangement. A vacuum region of 10 Å was inserted in the models to exclude periodic interaction between the slabs. Dipole corrections were also added in the direction normal to the surface.
The sampling of the Brillouin zone for all 3 x 3 surface cells was conducted with a k-point mesh of 5 x5 x 1 generated automatically using the Monkhorst Pack method[7]
Transition States
To locate the transition state, a series of 5 linearly interpolated images were formed between the reactant and the product state. The nudged elastic band method (NEB) [8] was used to locate the transition state. Once an approximate transition state was obtained, it was further refined using the climbing image nudged elastic band method (CI-NEB) [9]. Vibrational frequency calculations were then performed using IBRION = 7 in VASP to confirm the transition state found the first order saddle point. It was further ensured that the single imaginary frequency obtained was along the reaction pathway.
Results
Figure 1 illustrates the reactant, transition and product state for the hopping of Ag atom from the fcc to hcp site of Cu(111) surface. The activation barrier for the hopping process is 0.035 eV.

Figure 1. Top and Side view of the a) reactant b) transition c) product states for the Ag hopping from fcc site to the hcp site on Cu (111)
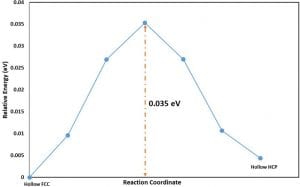
For the barrier evaluated using the CI-NEB method, the reactant and the product states were used to create a series of images. The energy profile obtained from the calculation for the images is shown below in Figure 2. (All energies are referenced to the reactant state and does not include zero- point vibrational energy corrections).
One important thing that was observed in a trial calculation is that the NEB method missed the transition state when 4 linearly interpolated intermediate images were used as shown in Figure 3. Using small even number of images can result in missing the saddle point and thus if using the NEB method, a higher density of images are needed near the saddle point. This highlights the need for caution when evaluating the activation barrier using the NEB method and using linear interpolation to obtain the images.

Figure 3. Reaction energy diagram obtained from the calculations using NEB method with 4 images obtained through linear interpolation
On an absolute scale, the zero-point vibrational energy (ZPVE) corrections were found to be very small. However, as the activation barrier itself is very small, we corrected the activation barrier by including the ZPVE corrections to the initial and the transition state. The corrected activation barrier after including the ZPVE corrections is 0.027 eV.
To evaluate the frequency of this hopping, we use the following equation:
where υi and υi† are the frequencies evaluated for reactant and transition state respectively, kB is the Boltzmann’s constant, ΔEact is the evaluated activation barrier and T is the temperature in Kelvin. As the transition state is first-order saddle point, it is energy minimum in all direction except for the reaction coordinate, along which it is maximum. Figure 4 shows the hopping frequency of Ag atom from fcc to hcp site on Cu(111) surface at different temperatures.

Figure 4. Frequency of hopping of Ag atom from fcc to hcp site on Cu(111) surface as a function of temperature
Conclusion
We used DFT methods to estimate the kinetic barrier for the hopping of Ag atom from the fcc to hcp site on Cu(111) surface. The activation barrier for this process after including the ZPVE corrections is found to be 0.027 eV. The value found is in reasonable agreement with the reported values [10]. This work illustrates the DFT methods can be used to evaluate kinetic parameters of the process. It also highlights that while using methods to evaluate the activation barrier, one should be careful and must ensure that the transition state found is the correct transition state. Vibrational calculations must be performed and a single imaginary frequency along the reaction coordinate must be confirmed to ensure that the transition state found is indeed the transition state we were looking for.
References
[1] G. Kresse, J. Furthmuller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 6 (1996) 15-50.
[2] G. Kresse, J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 54 (1996) 11169-11186.
[3] G. Kresse, D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B, 59 (1999) 1758-1775.
[4] J.P. Perdew, K. Burke, M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 77 (1996) 3865-3868.
[5] J.P. Perdew, J.A. Chevary, S.H. Vosko, K.A. Jackson, M.R. Pederson, D.J. Singh, C. Fiolhais, Atoms, Molecules, Solids, And Surfaces – Applications of the Generalized Gradient Approximation for Exchange and Correlation, Phys. Rev. B, 46 (1992) 6671-6687.
[6] M. Methfessel, A.T. Paxton, High-precision sampling for Brillouin-zone integration in metals, Physical Review B, 40 (1989) 3616-3621.
[7] H.J. Monkhorst, J.D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B, 13 (1976) 5188-5192.
[8] G. Henkelman, H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, The Journal of Chemical Physics, 113 (2000) 9978-9985.
[9] G. Henkelman, B.P. Uberuaga, H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, The Journal of Chemical Physics, 113 (2000) 9901-9904.
[10] Kotri, E. El koraychy, M. Mazroui, Y. Boughaleb, Static investigation of adsorption and hetero-diffusion of copper, silver, and gold adatoms on the (111) surface, Surface and Interface Analysis, 49 (2017) 705-711.