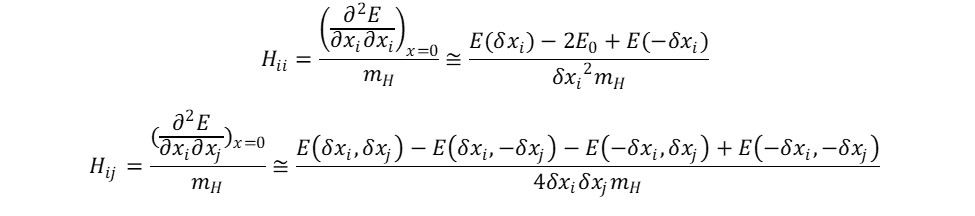by Brandon Bocklund
Introduction
Many of the observable properties that makes materials interesting are linked to the electronic structure, so it is desireable with to perform DFT calculations with the most accurate computational methods that are affordable. Calculations within DFT scale as \( \mathcal{O}(n^3) \) for n electrons [1], so many technologically important materials, including transition metals such as Fe, are computationally demanding to calculate when considering all the electrons. This is exacerbated for core electrons, since the wave functions near the nuclei tend to oscillate, requring a large number of plane waves required to describe the wave functions near the nuclear cores in extended systems. Since many key properties are influenced by the outermost valance electrons that control bonding, it is sensible to fix the core electrons and treat them approximately to make calculations of the same level of theory more affordable or to make more complex calulations affordable. Treating core electrons as fixed is known as the frozen core approximation.
In this post, different cutoff radii will be used to generate PAW datasets for Ti. Differences in the generated PAW datasets will be demonstrated by comparing the cutoff energy required to converge the energies of hcp Ti and by comparing the formation energy of TiO2.
Treating core electrons
Core and valence electrons
Typically there are two main parameters to consider when treating electrons as core or valence that effect how the wave functions will be constructed: the core radius and the number of core vs. valence electrons. The core radius is the spherical distance from the center of the atom that forms the outer bound for the approximation to the wave functions. The number of electrons in the core vs. valance is simply the partition of how many electrons of charge density an atom can contribute to bonding. For example, Ti has 22 electrons that must be partitioned between core and valance. Both of these parameters are typically chosen by the person developing the new description.
A basic description of some methods for treating core electrons in extended systems follows.
Pseudopotentials
Pseudopotentials replace the core wave functions with a pseudo wave function with the goal of defining a smooth function to represent the effective potential of the core. The pseudo wave function are constructed so that the value and the derivative of the pseudo wave function matches the value and derivative of the true wave functions at the core radius. The advantage of pseudopotentials is their formal simplicity, however the pseudo wave function prevents the recovery of the full core electron wave functions. James Goff published a post on pseudopotentials [2] that describes their construction in a detailed, introductory way.
LAPW
Another method for treating core electrons is the Linear Augmented Plane Wave (LAPW) method. The main idea of this method is that two partial waves, which can be used to describe the all-electron wave functions, are joined at the core radius and matched to the all-electron solution. Thus, the main advantage is the core wave functions can be recovered, but this method comes at a higher computational cost than the pseudopotential method. A more complete description of the pseuodpotential and LAPW methods can be found in [3].
PAW
The Projector Augmented Wave (PAW) method presented by Blöchl [4] as a formalism that generalizes and combines favorable aspects of the pseudopotential and LAPW methods through projector functions. The basis of the PAW method is the combination of partial wave functions from the isolated atom with pseudo partial waves. The PAW method defines a transformation operator that maps the pseudo wave functions onto the all-electron wave functions,
\begin{equation} \left| \Psi \right> = \mathcal{T} \left| \tilde\Psi \right> \end{equation}
for the all-electron wave function, \( \left| \Psi \right> \), the transformation operator, \( \mathcal{T} \), and the pseudo wave functions \( \left| \tilde\Psi \right> \). The transformation operator is defined as
\begin{equation} \mathcal{T} = 1+ \sum_i \left( \left| \phi \right> – \left| \tilde\phi \right> \right) \left< \tilde p_i \right|\end{equation}
where \( \left| \phi \right> \) and \( \left| \tilde\phi \right> \) are the all-electron partial waves and pseudo partial waves, respectively, and \( \left< \tilde p_i \right| \) are the projectors that are constructed to match the all-electron solution. In the PAW method, PAW datasets are generated that can recover the full core electron wave functions, like the LAPW method, but at a lower cost than the LAPW method, closer to the computational cost of pseudopotentials. More information can be found for the PAW method in [4-6] and more detailed description of the relationship between pseudopotentials, APW, and the PAW methods can be found in [4].
Calculation details
Calculations are performed using plane waves and the PBE functional implemented by Quantum Espresso [8] in the pwscf code. PAW datasets [4] are used to describe the core states. For Ti, PAW datastets are generated as part of this work with the ld1 code distributed with Quantum Espresso, based on the PS Library 1.0 parameterizations [9]. The PS Library 1.0 parameterization for O is used directly. The reference states for Ti and O are chosen as hcp Ti and the O2 molecule in a 10x10x10 fcc box. The size of the O2 box was converged to within 0.1 mRy. Detailed discussion of the convergence of the box size is out scope for this post.
The cutoff energy convergence of the different potentials are compared in the following sections below for Ti and TiO2. Oxygen cutoff energy was converged to 0.1 mRy at a wavefunction cutoff energy of 90 Ry and a kinetic energy cutoff of 720 Ry. For the calculation of formation energy, the maximum converged cutoff energy for each set of potentials is used across all structures. In all cases, Ti required a larger cutoff energy for convergence than O, so it was used for the calculations of TiO2.
The kpoint grids were converged to within 0.1 mRy. For hcp Ti, an 11x11x7 Monkhorst-Pack grid was used. For the O2 box, a 3x3x3 Monkhorst-Pack grid, and for rutile TiO2 a 4x4x7 grid. Showing the detailed kpoints convergence tests are out of scope for this study. Even though the different PAW datasets can lead to different electronic structures and kpoints convergence, a single set of kpoints for each set of structures were used across all of the different PAW datasets for simplicity.
For comparing the cutoff energy of hcp Ti, calculations with each PAW potential used the same structure, a hexagonal primitive cell with a lattice parameter of 5.8 a.u. and a c/a ratio of 1.58 (corresponding to the experimental c/a ratio). All static calculations were performed using tetrahedron integration and an energy convergence of 1e-8 Ry. For calculations of the formation energy, the cells and ionic positions for all cells (O, Ti for each potential, TiO2 for each potential) were relaxed with a force convergence criteria of 1e-9 Ry/bohr. The Brillouin zone integration for relaxations was treated with Gaussian smearing with a smearing width of 0.001 Ry.
Generating PAW datasets for Ti
The ld1 program was used to generate the PAW datasets. The documentation can be found online [10]. The starting point for the tests here is the input file for generating a PAW dataset for the spin polarized, scalar relativistic [12] Ti from the PS Library version 1.0.0 [9]. The input file for the PS Library starting point follows below. The settings here create a PAW dataset for Ti with Troullier-Martins pseudization [11] via Bessel functions. The the key inputs that will be changed is `rcore`, which is the matching radius in atomic units for the core charge smoothing. The bottom section describes the number of wave functions (6) that will be pseudized and which are described by the lines below. Taking the first line (3S) as the example, the first number is the principle quantum number (n=1, starting with 1 for the lowest s, 2 for the lowest p), then the angular momentum quantum number (l=0), followed by the number of occupying electrons, the energy used to pseudize the state (=0.00), the matching radius for the norm-conserving pseudopotential (=0.85), the matching radius for the ultrasoft pseudopotential (=1.30) and finally the total angular momentum (=0.0). Changing the norm-conserving or ultrasoft pseudopotential matching radii do not change the PAW dataset, since the radii are controlled by the input parameters above. Note that the energies for the unbound states (4p=4 Ry and unoccupied 3d=0.05 Ry) need to be non-zero.
&input title='Ti', zed=22., rel=1, config='[Ar] 4s2 4p0 3d2', iswitch=3, dft='PBE' / &inputp lpaw=.true., pseudotype=3, file_pseudopw='Ti-PSL.UPF', author='ADC', lloc=-1, rcloc=1.6, which_augfun='PSQ', rmatch_augfun_nc=.true., nlcc=.true., new_core_ps=.true., rcore=0.8, tm=.true. / 6 3S 1 0 2.00 0.00 0.85 1.30 0.0 4S 2 0 2.00 0.00 0.85 1.30 0.0 3P 2 1 6.00 0.00 0.80 1.60 0.0 4P 3 1 0.00 4.00 0.80 1.60 0.0 3D 3 2 2.00 0.00 0.80 1.50 0.0 3D 3 2 0.00 0.05 0.80 1.50 0.0
To demonstrate how the cutoff radius affects the calculation accuracy and expense (through the cutoff energy), two new PAW datasets will be generated with core radii of 0.4 a.u. (much smaller, further referred to as “small core”) and 2.0 a.u. (much larger, further referred to as “large core”). Note that these are note expected to be accurate, but instead to demonstrate how the parameters affect might affect calculations and impress the care and detail that should be given to generating proper potentials.
Energy cutoff convergence of Ti and formation energy TiO2
Figure 1a and 1b compre the relative and absolute energy convergence with respect to the wave function energy cutoff for the differently generated Ti PAW datasets. In Figure 1a, the PS Library converges at a wave function cutoff energy of 120 Ry, the large core at 110 Ry, and the small core does not converge to less than 0.1 mRy/atom even at 140 Ry. Computational demands and the instability of the PAW dataset limited the full convergence.
The cutoff energies follow the trend that would be expected. Compared to the default PS Libary PAW dataset, increasing the core radius allows for more of the wave function to be described by the core, and therefore the dataset is softer (requires smaller energy cutoffs). In addition, the small core is not converged even at 140 Ry because the smaller radius requires a harder potential with more plane waves being required to describe the wave function. Figure 1a also shows unusual behavior for the energy to not decrease variationally with the cutoff energy and instead shows that there was some osciallation in the energy with increasing energy cutoff. Note that the large core and the the PS Library default are quite close in energy, so the differences may be hard to see in both figures. Figure 1b aims to demonstrate that the energies for different pseudopotentials are different even for the same calculation settings, so they cannot be compared.

Figure 1a: Energy cutoff convergence relative to the energy calculated at a cutoff energy of 140 Ry. Energy differences are taken from 10 Ry to 140 Ry. Calculations not shown are outside the bounds of the plot.

Figure 1b: Energy convergence for cutoff energies ranging from 10 Ry to 140 Ry. Missing results at lower energy cutoff are off the scale of the plot.
As discussed previously, energies between different pseudopotentials cannot be directly compared, therefore a metric that can cancel the differences is desired. The formation energy of TiO2 can cancel the differences caused by the different treatment of Ti and give some insight into the practical implications of different treatments of the electronic structure. Using the cutoff energies found for Ti (120 Ry for PS Library, 140 Ry for small core, 110 Ry for the large core) the energies per atom of hcp Ti, O2 in a vaccuum box, and TiO2 are calculated. The formation energy of TiO2 is calculated in the usual way:
\begin{equation} E^\mathrm{form} = E_{\mathrm{TiO_2}} – (E_{\mathrm{Ti}} + E_{\mathrm{O_2}}) \end{equation}
Since in each case, the cutoff energies are convered for all calculations within each formation energy calculation, the formation energies can be safely compared even with different cutoff energies used between them.
| Structure | PS Library | Small core | Large core |
|---|---|---|---|
| hcp Ti (Ry/atom) | -183.6910 | -183.6974 | -183.6975 |
| O (Ry/atom) | -41.4776 | -41.4776 | -41.4776 |
| TiO2 (Ry/atom) | -89.1361 | -89.1363 | -89.1357 |
| TiO2 formation (Ry/atom) | -0.2541 | -0.2521 | -0.2515 |
The total energies and formation energies are shown in Table 1. The differences in the formation energy are larger than the convergence criteria (0.1 mRy/atom, 0.0001 Ry/atom) for the formation energies of the PS Library to the small core PAW dataset and the PS Library to the large core PAW dataset. The largest difference is 0.0026 Ry/atom for the small core and PS Library formation energies, which corresponds to above 3 kJ/mole-atom. Differences that large could impact the relative stability of TiO2 in a more comprehensive study that used inaccurate PAW datasets.
Conclusion
PAW datasets were reviewed in context of other types of frozen core approximations, then PAW datasets were generated for Ti with larger and smaller core radii than the ones parameterized in the PS Library v1.0.0. It was shown that the different core radii can affect the energy cutoff convergence, the total energy, and the formation energy of a compund, TiO2.
References
[1] Section 10.5, D.S. Sholl, J.A. Steckel, Density Functional Theory, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2009. doi:10.1002/9780470447710.
[2] J. Goff, Transferability of Cu Pseudopotentials in Cu/CuO Systems, Density Funct. Theory Pract. Course. (2019). https://sites.psu.edu/dftap/2019/03/31/transferability-of-cu-pseudopotentials-in-cucuo-systems/.
[3] D.J. Singh, L. Nordstrom, Planewaves, Pseudopotentials and the LAPW Method, Second Edi, Springer US, 2006. doi:10.1007/978-0-387-29684-5.
[4] P.E. Blöchl, Projector augmented-wave method, Phys. Rev. B. 50 (1994) 17953–17979. doi:10.1103/PhysRevB.50.17953.
[5] X. Gonze, F. Finocchi, Pseudopotentials Plane Waves-Projector Augmented Waves: A Primer, Phys. Scr. T109 (2004) 40. doi:10.1238/physica.topical.109a00040.
[6] R.M. Martin, Electronic Structure: Basic Theory and Practical Methods, Cambridge University Press, 2004. doi:10.1017/CBO9780511805769.
[7] J.P. Perdew, K. Burke, M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett. 77 (1996) 3865–3868. doi:10.1103/PhysRevLett.77.3865.
[8] P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G.L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A.P. Seitsonen, A. Smogunov, P. Umari, R.M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials., J. Phys. Condens. Matter. 21 (2009) 395502. doi:10.1088/0953-8984/21/39/395502.
[9] A. Dal Corso, Pseudopotentials periodic table: From H to Pu, Comput. Mater. Sci. 95 (2014) 337–350. doi:10.1016/j.commatsci.2014.07.043.
[10] http://web.mit.edu/espresso_v6.1/amd64_ubuntu1404/qe-6.1/Doc/INPUT_LD1.html
[11] N. Troullier, J.L. Martins, Efficient pseudopotentials for plane-wave calculations, Phys. Rev. B. 43 (1991) 1993–2006. doi:10.1103/PhysRevB.43.1993.
[12] Koelling, D. D. & Harmon, B. N. A technique for relativistic spin-polarised calculations. J. Phys. C Solid State
Phys. 10, 3107–3114 (1977).